Division of Rational Expressions

Key Questions

• How does the division of rational expressions differ from the multiplication of rational expressions?

  Multiplication

  #a/b cdot c/d={a cdot c}/{b cdot d}#

  Division

  #a/b divide c/d=a/b cdot d/c={a cdot d}/{b cdot c}#

  ---

  I hope that this was helpful.

  Wataru · 1 · Oct 26 2014
• How do you divide rational expressions?

  Remember that dividing by a fraction is equivalent to multiplying by the reciprocal of the fraction, that is,

  #a/b divide c/d = a/b cdot d/c={a cdot d}/{b cdot c}#

  ---

  I hope that this was helpful.

  Wataru · 1 · Nov 6 2014
• How do you divide 3 rational expressions?

  I would just turn it into multiplications.

  #a/b divide c/d divide e/{f} = a/b times d/c times f/e={a cdot d cdot f}/{b cdot c cdot e}#

  ---

  I hope that this was helpful.

  Wataru · 1 · Nov 11 2014
• What is Division of Rational Expressions?

  Division of a rational expression are similar to fractions.For dividing rational expressions, you will use the same method as you used for dividing numerical fractions: when dividing by a fraction, you flip-n-multiply. For instance:

  #[ (x^2 + 2x - 15) / (x^2 - 4x - 45) ] ÷ [ (x^2 + x - 12) / (x^2 - 5x - 36) ]#

  

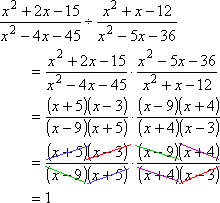  here as you see i have factored the different expressions and cancelled the common expression finally it gets reduced to nothing

  Hope this helped you

  Sidharth · 3 · Jan 5 2015

• What is Division of Rational Expressions?
• How does the division of rational expressions differ from the multiplication of rational expressions?
• How do you divide 3 rational expressions?
• How do you divide rational expressions?
• How do you divide and simplify #\frac{9x^2-4}{2x-2} -: \frac{21x^2-2x-8}{1} #?
• How do you divide and reduce the expression to the lowest terms #2xy \-: \frac{2x^2}{y}#?
• How do you divide #\frac{x^2-25}{x+3} \-: (x-5)#?
• How do you divide #\frac{a^2+2ab+b^2}{ab^2-a^2b} \-: (a+b)#?
• How do you simplify #(w^2+6w+5)/(w+5)#?
• How do you simplify #(x^4-256)/(x-4)#?
• How do you simplify #(x^2-9)/(x+2)div(x^2+x-6)/(x^2-4)#?
• How do you simplify #(x^-1-y^-1)/(x^2-y^2)#?
• How do you simplify #(x^3 - 9x) / (x^2 - 7x + 12)#?
• How do you simplify #(x/y - y/x)/(1/y + 1/x)# and can you use a calculator to simplify?
• How do you simplify #(-2y+6)/(-4y)#?
• How do you simplify #(2x^2+6x+4)/(4x^2-12x-16)#?
• How do you simplify #(9x + 10xy) / x#?
• How do you simplify #(14a^2b + 35ab^2) / (7ab)#?
• How do you simplify #(25c^3d^3e^3 - 55c^4d^5e^7 + 35c^8d^7e^6) / (5c^2d^2e^3)#?
• How do you simplify #(12a^2bx)/(30ax^2)#?
• How do you simplify #(14y^3)/(7y)#?
• How do you simplify #(9a^4bx^3)/(abx^2)#?
• How do you simplify #(8mn^2)/(4m)#?
• How do you simplify #(15a^2b^2 )/(5ab)#?
• How do you simplify #(20mn^2 )/(5n^2)#?
• How do you simplify #b^19/b^12#?
• How do you simplify #(5y-10)/-5#?
• How do you simplify #(3y^2 - y + 4)/(y^3)#?
• How do you simplify #(3a^7 - a^5 + 5a^3)/(a^2)#?
• How do you simplify #(9b^6 - 6b^3 + 2)/(3b^3)#?
• How do you simplify #(4x^2+2x-1 )/( x+3 )#?
• How do you simplify #(6x^2-x+6 )/( 2x-1 )#?
• How do you simplify #(2x^3-14x+2 )/(x+3)#?
• How do you simplify #(x^2n-1)/( x^n-3)#?
• How do you multiply #(3x^2-1)/(4x(x-5)) div ((3x^2)(x-1))/(x-5)#?
• How do you multiply #(m+3)/(4m) div (m^2-9)/(32m^2(m-3))#?
• How do you multiply #(48s^3+36s^2)/(9s(s^2-3s-10)) xx (16s+12)/(s^2-7s+10)#?
• How do you simplify #(6y^3 - 12y^2) /(12y^2 - 18)#?
• How do you divide #(t^2-16)/(t^2-8t+16)#?
• How do you simplify #(x^2 – 3x – 10)/(x^2 – 9)div(x^2 + 4x + 4)/(x+3)##?
• How do you divide #(5x-5)/16div(x-1)/6#?
• How do you divide #(x^2-9)/(4x+12)div(x-3)/6#?
• How do you divide #(x^2+13x+12)/(x+2)div(x+1)#?
• How do you simplify #(6x – 9) /(5x +1)div(6 – 13x + 6x^2)/(15x^2 - 7x – 2)#?
• How do you divide #2/(m(m+3)) *( 3m + 9)/6#?
• How do you divide #(x^3+27)/(9x+27) div(3x^2-9x+27)/(4x)#?
• How do you divide #(x^2+5x+6)/(x-4) div (x^2-4x-21) /(x-4)#?
• How do you divide #(x+9)/(x-1) div(3)/(5)#?
• How do you divide #(5x+15)/(12x-6) div(10x^2)/(18)#?
• How do you divide # (5x^2)/(3) div(10x)/(2)#?
• How do you divide # (x^2-5x-14)/(x-7)div(x+2)/(x^2-9)#?
• How do you divide # (x^2-5x-14)/(x-7)div(x+2)/(x^2-9)#?
• How do you simplify #(1/x) / ((3x)/5)#?
• How do you simplify #(6t^3 + 5t^2 + 9) / (2t + 3)#?
• How do you simplify #(3m^2 + 9m + 6) / (4m^2 + 12m + 8)#?
• How do you simplify #a^5/(b^3c^3) div a^4/(b^3c^4)#?
• How do you simplify #(6y)/(y^2+y-72) div y^6/(8-y)#?
• How do you simplify #(x^2-7x+12)/(x^2-25) div (x-4)/(x-5)#?
• How do you simplify #(k^2-4)/(3k^2) ÷ (2-k)/(11k)#?
• How do you simplify #(8a^2-6a-9)/( 6a^2-5a-6) ÷ (4a^2+11a+6)/( 9a^2+12a+4)#?
• How do you simplify #[(2x^3+3x^2-2x)/( 3x-15) ÷ (2x^3-x^2)/ (x^2-3x-10)] * (5x^2-10x)/(3x^2+12x+12)#?
• How do you simplify #(6x-3)/5 div (4x-8)/25#?
• How do you simplify #(x^3 - 64)/(x^3 + 64) div (x^2 - 16)/(x^2 - 4x + 16)#?
• How do you simplify #(x^2+4x-5)/(5x^2-8x+3) div (20x-12)/(x^2-6x-55)#?
• How do you simplify #(8x-56)/(x^2-49)div(x-6)/(x^2+11x+28)#?
• How do you simplify #(6x^2-54x+84)/(8x^2-40x+48) div (x^2+x-56)/(x^2+12x+32)#?
• How do you simplify #(x+3) /( x+1) div (x^2+5x+6)#?
• How do you simplify #(2x+4 )/( x^2+11x+18) div( x+1) /( x^2+14x+45)#?
• How do you simplify #(2p^3q^2)/(8p^4q) div (4pq^2)/(16p^4)#?
• How do you simplify #(15-14x-8x^2)/ (4x^2 +4x-15) div ( 4x^2+13x-12)/(3x^2+16x+5)#?
• How do you simplify #(9x^2-16)/ (6x^2-11x+4) div ( 6x^2+11x+4)/(8x^2+10x+3)#?
• How do you simplify #(5x-5)/16 div (x-1)/6#?
• How do you simplify #(6-3x)/5 div(4x-8)/25#?
• How do you simplify #(x^2-12x+32)/(x^2-6x-16) div (x^2-x-12)/(x^2-5x-24)#?
• How do you simplify #(7a^2b)/(9ab^3) div (3a^4)/(2a^2b^2)#?
• How do you simplify #(16x^2y)/(24xy^3) div (9xy)/(8x^2y^2)#?
• How do you simplify #(x^2 - 16 )/( 2x^2 - 9x + 4) div (2x^2 + 14x + 24) /( 4x + 4)#?
• How do you simplify #(x^2-y^2)/(xy+x^2) div (y-x)/(x+y)#?
• How do you simplify #(15a+5b)/(5ab) div 3a+b#?
• How do you simplify #(x-8)^2/12 ÷ (12x - 96)/144 #?
• How do you divide #(v^3+27)/(v+3)#?
• Question #e806e
• How do you simplify #(4y + 8 )/(y^2 + 7y + 10)#?
• How do you simplify #(4y + 8 )/(y^2 + 7y + 10)#?
• How do you simplify #(x^2-4)/(x^2-7x+10) div (x^2+6x+5)/(x^2-25)#?
• How do you simplify #5/(6x^3 + x)div(x^2-12x)#?
• What is the quotient: #(2x^3 – 13x^2 + 16x – 5) ÷ (x – 5)# ?
• What is the quotient: #(x^3 - 5x^2 + 3x - 8 ) ÷ (x – 3)# ?
• How do you simplify #(x^2 - 4x + 4 - y^2)/( 2x^2 - 11x + 15) * (x^4 y)/ (x- 2 + y) div (x^3 y - 2x^2y - x^2 y^2)/( 3x -9)#?
• How do you simplify #(x^2 – 6x – 7 )/( x^2 – 1)#?
• How do you simplify #x/(x+xy)#?
• How do you simplify #(c/a+c/b) / (c/(ab))#?
• How do you simplify #(1-(3/x) )/ ((x/12)-(1/4))#?
• How do you simplify #(y/3 + 1)/(y^2/9 - 1)#?
• How do you simplify the rational expression: #(m^2+10m+24)/(m+4)#?
• How do you simplify #((1/x) - (1/5))/((1/x^2) - (1/25))#?
• How do you simplify #(9 - x^(-2))/(3 + x^(-1))#?
• How do you simplify #(9x-21)/(15x-35)#?
• How do you simplify #(6-2x)/( 4x-12)#?
• How do you simplify #(x^3+1)/(x+1)#?
• How do you simplify and state the excluded values for #(4x-4)/(x-1)#?
• How do you simplify #(-6c^3)/(2c^4 8c^2)#?
• How do you divide #(s^2-3s)/(s^2-s-6) div (s-6)/(s+2)#?
• How do you divide #(-10m^7+14m^6-10m^5) div 2m^3#?
• How do you divide #(25x^2-30x+12) div (5x-3)#?
• How do you divide #(6x^3-12x+10) div (3x-3)#?
• How do you simplify #(3x+4)/12 div 8/(9x+12)#?
• How do you divide #(x^3-1)/(x^2+1) div (9x^2+9x+9)/(x^2-x)#?
• How do you simplify #(x-3)/(x-5) div (x^3-27)/(x^3+8)*(x^2-25)/(x + 5)#?
• How do you simplify #((x^2-y^2)(x^2+xy+y^2))/((x^3-y^3)(x^2+2xy+y^2))#?
• How do you simplify #((10ab)/(x² - y²)) / ((5a(x - y))/(3ax(x + y))#?
• How do you simplify #(2x^(3)-4x^(2)+12x+18)/(x+1)#?
• How do you simplify #2/(x-2) div (x-1)/(4x - 8)#?
• How do you divide # {(12m^2n^5)/(m+5)}/{(3m^3n)/(m^2-25)}#?
• How do you divide #{(n^2-n-12)/(2n^2-15n+18)}/{(3n^2-12n)/(2n^3-9n^2)}#?
• How do you divide #{(17mn^3)/(m^2+2m-35)}/{(34m^8n^4)/(m^2+7m)}#?
• How do you divide #{(16-2m)/(m^2+2m-24)}/{(m-8)/(3m+18)}#?
• What is the result if you divide #-12x^8y^8# by #3x^4y^2#?
• How do you rationalize the denominator and simplify #1/ (x(1-sqrt x) ) #?
• How do you factor #(4x^2+16x+15)/(2x^2+x-3)#?
• How do you factor #(3x^2+4x-15)/(2x^2+3x-9)#?
• How do you factor #(x^2-14x+49)/(x^2-2x-35)#?
• How do you factor #(x^2-81)/( 2x^2-23x+45)#?
• How do you factor #(7x^2+11x-6)/(x^2-4)#?
• How do you simplify #(x^2-5x+4)/(x^2-x-12)#?
• How do you simplify #(5/(4x^2)) / (8/x^3)#?
• How do you simplify #((x-5)/(x+3)) /(( x-2)/(x+3))#?
• How do you simplify #((4x+16)/(x / (x+4)))#?
• How do you divide: #(x^3 - 6x^2 + 12x - 8) ÷ (x - 2)#?
• How do you simplify #(28n^2-175) / (2n^2-7n+5) div(14n^2+31n-10 )/ (n^2-6n+5)#?
• How do you simplify #(24x^4)/(15x)#?
• How do you simplify #(-91a^4b+14ab )/ (-7ab)#?
• How do you simplify #(x^2+3x+2)/(x^2-1)#?
• How do you simplify #(4x^3 )/(2x^2)div (x^2-9)/( x^2-4x-21)#?
• How do you simplify #(x²-7x+6)/ (x²-1) div(2x²-12x)/(x+1)#?
• How do you simplify #(m^2-9mn+14n^2 )/(m^2+7mn+12n^2 )#?
• How do you simplify #(x^2-8x+16 )/(x^2-12x+32 )#?
• How do you simplify #(2x) /( x + 4) div (6)/(x-1)#?
• How do you simplify #x^2/3 divx^4/9 #?
• How do you simplify and find the excluded value of #(x^2 – 3x + 2)/( 7x – 14) div(x^2 – 1)/(7x + 7)#?
• How do you simplify # (10ab+10b)div(10b)#?
• How do you simplify the expression #(16x^4y-12x^5y^3)/(2x^3y^2)#?
• How do you simplify the expression #(12m^4-24m^3+6m^2+9m-9)/(6m^2)#?
• How do you simplify #[1/(3+x) - 1/3] / x#?
• How to simplify this?
• How do you simplify #(4a^2+11a+6)/(a^2+4a+4) ÷ (4a^2-5a-6)#?
• How do you simplify #(10a^2+11a-6) ÷ (16-a^2)/(5a^2+18a-8)#?
• How do you simplify #(2a^2+ab-b^2)/(a^3+b^3) ÷ (2a^2b^2-ab^3)/(2a^2-2ab+2b^2)#?
• How do you simplify #(3a^2-ab-2b^2)/(a^3b^3 )÷ (15a^2+10ab)/(5a^2+5ab+10b^2)#?
• How do you simplify #(4x^2-9)/(2x^2+11x+12)# to lowest terms?
• How do you simplify #(8x)/ (x^2-4) div (4x^2)/ (x^2+4x+4)#?
• How do you divide #(3x^2 + 5x + 7) / (x + 1) #?
• How do you simplify #((x/y)-(y/x))/((1/y)-(1/x))#?
• How do you simplify #((x^2-2x-4)/(x^2+2x-8))*((3x^2+15x)/(x+1))/((4x^2-100)/(x^2-x-20))#?
• How do you simplify #(v^2 + v - 12)/ (v^2 + 6v + 8) div (2v - 6)/( v +2)#?
• How do you simplify #[(x-a)+(2a^2)/(x+a)] * [((1/x^2)-(1/a^2))] div[((x^3)-((ax^3+a^4)/(x+a)))]#?
• How do you simplify #(x/9 - 1/x) / (1+ 3/x) #?
• How do you simplify #((1/(3+h)) - (1/3)) / h#?
• How do you simplify #(x^2-25) / (2x) div (x^2 + 6x+5) / (4x^2)#?
• How do you simplify # (9x^2-15xy)/(9x^2-25y^2)#?
• How do you simplify #(1 - 2/a)/(4/(a^2 - 1))#?
• How do you simplify #((1 - m)/m)/(m - 1/m)#?
• Question #f220a
• How do you simplify #(x+5)/(x-5) div (x^2-25)/(5-x)#?
• How do you simplify # (1+1/x)/(1/x)#?
• How do you simplify and find the restrictions for #((3x)/y -x/1) / ((2y)/1 - y/x)#?
• How do you simplify and find the restrictions for #( (x^2 -x-12)/( x^2 -2x-15) ) / ( (x^2 + 8x+12)/( x^2 -5x-14))#?
• How do you simplify #(2a^2- 3a-9) /( 8a^2+14+3) div(3a^2-7a-6)/(8a^2+14a+3)#?
• How do you simplify #((x/y) - (4/x)) / ((1/x) - (2/y^2))#?
• How do you divide #3x^3 - 3x^2 - 4x + 3# by x + 3?
• How do you find the remainder when #x^3+3x^2+3x+1# is divided by 5+2x?
• How do you simplify # [ (1/x) - (1/2) ] / [ x- 2 ]#?
• How do you simplify #(4x+16)/x div (x+4)#?
• How do you simplify #(-2x+34)/(-4x+6)#?
• How do you multiply #(5x)/7 div(10x^2)/21#?
• How do you multiply #(2a)/(7b^3)div(10a^5)/77#?
• How do you multiply #(6x^2y^2)/(x-2) div (3xy^2)/(x-2)^2#?
• How do you multiply #(r+3)^2/(4r^3s)div(r+3)/(rs)#?
• How do you multiply #(t^2+5t)/(t+1)div(t+5)#?
• How do you multiply #(6p+7)/(p+2)div(36p^2-49)#?
• How do you multiply #a/(a-10)div(a^3+6a^2-40a)/(a^2-100)#?
• How do you multiply #(b^2-6n+9)/(b^2-b-6)div(b^2-9)/4#?
• How do you multiply #(2x^2+5xy+2y^2)/(4x^2-y^2)div(x^2+xy-2y^2)/(2x^2+xy-y^2)#?
• How do you multiply #(x^4-x^3+x^2-x)/(2x^3+2x^2+x+1)div (x^3-4x^2+x-4)/(2x^3-8x^2+x-4)#?
• How do you multiply #(3y-y^2)/(y^3-27) div y/(y^2+3y+9)#?
• How do you multiply #(8x-4x^2)/(xy-2y+3x-6) div (3x+6)/(y+3)#?
• How do you multiply #(8a^4b^3)/(3c) div (a^7b^2)/(9c)#?
• How do you multiply #2/(25x^2)*(5x)/12div2/(15x)#?
• How do you multiply #(4y)/7divy^2/14*3/y#?
• How do you multiply #(3m^2-12m)div(m^2-4m)/(m^2-6m+8)#?
• How do you multiply #(2x^2+8)div(x^4-16)/(x^2+x-6)#?
• How do you multiply #(a+b)^2/(a-b)*(a^3-b^3)/(a^2-b^2)div(a^2+ab+b^2)/(a-b)^2#?
• How do you simplify #(x^2-3x-40)/(5x)div (x+5)#?
• How do you simplify #(8/x+11)/(1/(6x)-1)#?
• How do you simplify #(36-1/x^2)/(1/(6x^2)-6)#?
• How do you simplify #(2/(x^2-1)-1/(x+1))/(1/(12x^2-3)#?
• How do you simplify #(1/(x-5)-x/(x^2-25))/(5/(2x))#?
• How do you simplify #(144)/(4xy)div (54y^3)/(3x^3y)#?
• How do you simplify #(16xy)/(3x^5y^5)div (8x^2)/(9xy^7)#?
• How do you simplify #(5x^2+10x)/(x^2-x-6)div(15x^3+45x^2)/(x^2-9)#?
• How do you simplify #(32x^3y)/y^9div(8x^4)/y^6#?
• How do you simplify #(2xyz)/(x^2z^2)div (6y^3)/(3xz)#?
• How do you simplify #(3x^2+x-2)/(x^2+3x+2)div (2x)/(x+2)#?
• How do you simplify #(x^2-14x+48)/(x^2-6x)div(3x-24)#?
• How do you simplify #(2x^2-12x)/(x^2-7x+6)div(2x)/(3x-3)#?
• How do you simplify #(x^2+8x+16)/(x+2)div(x^2+6x+8)/(x^2-4)#?
• How do you simplify #(x^2+6x-7)/(3x^2)div(x+7)/(6x)#?
• How do you simplify #(x^2+6x-27)div(3x^2+27x)/(x+5)#?
• How do you simplify #(x-5)div(x^2-11x+30)/(x^2+7x+12)*(x-6)#?
• How do you simplify #(x^2-x-12)/(8x^2)div(x^3+3x^2)/(8x^3-2x^2)div(4x-1)/(x+2)#?
• How do you simplify #(x^2+11x)/(x-2)div(3x^2+6x)*(x^2-4)/(x+11)#?
• How do you simplify #(2x^2+x-15)/(2x^2-11x-21)*(6x+9)div(2x-5)/(3x-21)#?
• How do you simplify #(x^3+8)*(x-2)/(x^2-2x+4)div(x^2-4)/(x-6)#?
• How do you simplify #(x^2+12x+20)/(4x^2-9)*(6x^3-9x^2)/(x^3+10x^2)*(2x+3)#?
• How would you find the domain of each: #y=(3x+2)/(4x+1)#? #y=(x^2-4)/(2x+4)#? #y=(x^2-5x-6)/(x^2+3x+18)#? #y=(2^(2-x))/(x)#? #y=sqrt(x-3)-sqrt(x+3)#? #y=sqrt(2x-9)/(2x+9)#?
• How would you find the equations of both the horizontal and vertical asymptotes for the following functions: #y=(x)/(x-3)#? #y=(x+4)/(x^2-1)#? #y=(x+4)/(x^2-1)#? #y=(x^2-2x+1)/(x^2-3x-4)#? #y=(x^2-9)/(x^2-3x^2-18x)#?
• Question #22c29
• Question #60e34
• The volume of a rectangular prism is #3x^3+34x^2+72x-64#, if the height is x+4, what is the area of the base of the prism?
• How do you simplify #(15x^4y^2)/(40x^3y^3)# and what are the ecluded values fot he variables?
• How do you simplify #(32n^2p)/(2n^4p)# and what are the ecluded values fot he variables?
• How do you simplify #((4t^3)(2t))/(20t^2)# and what are the excluded values for the variable?
• How do you simplify #((7c^2)(-6c^3))/(21c^4)# and what are the excluded values for the variables?
• How do you simplify #(4x-24)/(x^2-12x+36)# and what are the ecluded values fot he variables?
• How do you simplify #(a^2+3a)/(a^2-3a-18)# and what are the ecluded values fot he variables?
• How do you simplify #(u^2+7u-18)/(u-2)# and what are the excluded values for the variables?
• How do you simplify #(x^2+4x-32)/(x+8)# and what are the ecluded values fot he variables?
• How do you simplify #(x^2-25)/(x^2+5x)# and what are the ecluded values fot he variables?
• How do you simplify #(2p^2-14p)/(p^2-49)# and what are the ecluded values fot he variables?
• How do you simplify #(2x-10)/(25-x^2)# and what are the excluded values for the variables?
• How do you simplify #(64-c^2)/(c^2-7c-8)# and what are the ecluded values fot he variables?
• How do you find the quotient of #8/(3x^2)div4/x#?
• How do you find the quotient of #c^5/2divc^3/(6d^2)#?
• How do you find the quotient of #(b^2+6b+5)/(6b+6)div(b+5)#?
• How do you find the quotient of #(2x+8)/(x+3)div(x+4)/(x^2+6x+9)#?
• How do you find the quotient of #x^5/ydivx/y^2#?
• How do you find the quotient of #(3r^4)/k^2div(18r^3)/k#?
• How do you find the quotient of #(21b^3)/(4c^2)div7/(6c^2)#?
• How do you find the quotient of #(r^4g^2h)/(x^2y)divf^3g#?
• How do you find the quotient of #(6b-12)/(b+5)div(12b+18)#?
• How do you find the quotient of #(k+3)/(k+2)divk/(5k+10)#?
• How do you find the quotient of #(5x^2)/(x^2-5x+4)div(10x)/(x-1)#?
• How do you find the quotient of #(n&2+7n+12)/(16n^2)div(n+3)/(2n)#?
• How do you find the quotient of #(r+2)/(r+1)div4/(r^2+3r+2)#?
• How do you find the quotient of #(3a)/(a^2+2a+1)div(a-1)/(a+1)#?
• How do you find the quotient of #(8a^2+20a)div4a#?
• How do you find the quotient of #(4z^3+1)div2z#?
• How do you find the quotient of #(12n^3-6n^2+15)div6n#?
• How do you find the quotient of #(t^2+5t+4)div(t+4)#?
• How do you find the quotient of #(x^2+3x-28)div(x+7)#?
• How do you find the quotient of #(x^2+x-20)div(x-4)#?
• How do you find the quotient of #(n^2+3n+10)div(n-1)# using long division?
• How do you find the quotient of #(4y^2+8y+3)div(y+2)# using long division?
• How do you find the quotient of #(4h^3+6h^2-3)div(2h+3)# using long division?
• How do you find the quotient of #(9n^3-13n+8)div(3n-1)# using long division?
• How do you find the quotient of #(14x^2+7x)div7x#?
• How do you find the quotient of #(a^3+4a^2-18a)diva#?
• How do you find the quotient of #(5q^3+q)divq#?
• How do you find the quotient of #(6n^2-12n+3)div3n#?
• How do you find the quotient of #(8k^2-6)div2k#?
• How do you find the quotient of #(9m^2+5m)div6m#?
• How do you find the quotient of #(a^2+a-12)div(a-3)#?
• How do you find the quotient of #(x^2-5x-16)div(x+2)#?
• How do you find the quotient of #(r^2-12r+11)div(r-1)#?
• How do you find the quotient of #(k^2-5k-24)div(k-8)#?
• How do you find the quotient of #(y^2-36)div(y^2+6y)#?
• How do you find the quotient of #(a^3-4a^2)div(a-4)#?
• How do you find the quotient of #(c^3-27)div(c-3)#?
• How do you find the quotient of #(4t^2-1)div(2t+1)#?
• How do you find the quotient of #(6x^3+16x^2-60x+39)div(2x+10)#?
• How do you find the quotient of #(2h^3+8h^2-3h-12)div(h+4)#?
• How do you find the quotient of #(b^3+3b-9)div(b+5)# using long division?
• How do you find the quotient of #(a^2+4a+3)div(a-1)# using long division?
• How do you find the quotient of #(4n^2-3n+6)div(n-2)# using long division?
• How do you find the quotient of #(p^3-4p^2+9)div(p-1)# using long division?
• How do you find the quotient of #(t^3-2t-4)div(t+4)# using long division?
• How do you find the quotient of #(6x^3+5x^2+9)div(2x+3)# using long division?
• How do you find the quotient of #(8c^3+6c-5)div(4c-2)# using long division?
• How do you find the quotient of #(x^3+11x+14)div (x+2)# using long division?
• How do you find the quotient of #(14y^5+21y^4-6y^3-9y^2+32y+48)div(2y+3)# using long division?
• If the quotient of two polynomials is #4x^2-x-7+(11x+15)/(x^2+x+2)#, what are the two polynomials?
• How do you find the quotient #(6x^2+10x)div2x#?
• How do you find the quotient #(15y^3+14y)div3y#?
• How do you find the quotient #(10a^3-20a^2+5a)div5a#?
• How do you find the quotient #12/(3x^2)div6/x#?
• How do you find the quotient #g^4/2divg^3/(8d^2)#?
• How do you find the quotient #(4y-8)/(y+1)div(y-2)#?
• How do you find the quotient #2/n+4#?
• How do you write the mixed expression #r+1/(3r)# as a rational expression?
• How do you write the mixed expression #6+5/(t+1)# as a rational expression?
• How do you write the mixed expression #(x+7)/(2x)-5x# as a rational expression?
• How do you simplify #(2 1/3 )/(1 2/5)#?
• How do you simplify #(4/5)/(6 2/3)#?
• How do you simplify #(a^2/b^3)/(b^5/a)#?
• How do you simplify #(y^4/x^2)/((xy^2)/(2x^2))#?
• How do you simplify #(6/(x-2))/(3/(x^2-x-2))#?
• How do you simplify #((r+s)/(x^2-y^2))/((r+s)^2/(x-y))#?
• How do you simplify #((p+3)/(p^2+p-6))/((p^2+4p+3)/(p^2+6p+9))#?
• How do you write the mixed expression #10+6/f# as a rational expression?
• How do you write the mixed expression #p-7/(2p)# as a rational expression?
• How do you write the mixed expression #5a-(2a)/b# as a rational expression?
• How do you write the mixed expression #3h+(1+h)/h# as a rational expression?
• How do you write the mixed expression #t+(v+w)/(v-w)# as a rational expression?
• How do you write the mixed expression #n^2+(n-1)/(n+4)# as a rational expression?
• How do you write the mixed expression #(k+2)+(k-1)/(k-2)# as a rational expression?
• How do you write the mixed expression #(d-6)+(d+1)/(d-7)# as a rational expression?
• How do you write the mixed expression #(h-3)/(h+5)-(h+2)# as a rational expression?
• Ebony read 6 3/4 pages of a book in 9 minutes, what is her average reading rate in pages per minute?
• How do you simplify #(2 2/9)/ (3 1/3)#?
• How do you simplify #(5 3/5)/ (2 1/7)#?
• How do you simplify #(g^2/h)/(g^5/h^2)#?
• How do you simplify #((5n^4)/(p^3))/((6n)/(5p))#?
• How do you simplify #(2/a)/(1/(a+6))#?
• How do you simplify #((t+5)/9)/((t^2-t-30)/12)#?
• How do you simplify #((j^2-16)/(j^2+10j+16))/(15/(j+8))#?
• How do you simplify #((x-3)/(x^2+3x+2))/((x^2-9)/(x+1))#?
• The centralville high school cooking club has 12 1/2 pounds of flour with which to make tortillas, there are 3 3/4 cubs of flour in one pound, and it takes about 1/3 cup of flour per tortilla, how many tortillas can they make?
• How do you simplify the expression #15-(17x+5)/(5x+10)#?
• How do you simplify the expression #(b/(b+3)+2)/(b^2-2b-8)#?
• How do you simplify the expression #(1+(2c^2-6c-10)/(c+7))/(2c+1)#?
• How do you simplify the expression #(y-12/(y-4))/(y-18/(y-3))#?
• How do you simplify the expression #((x^2-4x-32)/(x+1))/((x^2+6x+8)/(x^2-1))#?
• How do you simplify the expression #((r^2-9r)/(r^2+7r+10))/((r^2+5r)/(r^2+r-2))#?
• How do you simplify the expression #(y/x-x/y)/((x+y)/(xy))#?
• How do you simplify the expression #(1/(t-1)+1/(t+1))/(1/t-1/t^2)#?
• How do you write a complex fraction that when simplified results in 1/x?
• How do you find the quotient #a^2+4a-22 div a-3# using long division?
• How do you find the quotient #(3q^2+20q+11)div(q+6)# using long division?
• How do you find the quotient #(3y^3+8y^2+y-7)div(y+2)# using long division?
• How do you find the quotient #(6t^3-9t^2+6)div(2t-3)# using long division?
• How do you find the quotient #(9h^3+5h-8)div(3h-2)# using long division?
• How do you write the rational expression in lowest terms #(4p(p+4))/(20p^2 (p- 4))#?
• How do you simplify #(-5/x)/(1/4)#?
• How do you simplify #x/(x^2+1)divx/(x^4-1)# and state the domain?
• How do you simplify #(9x^3)/(12x-24)div(x^2+4x)/(x-2)#?
• How do you simplify #(x/4-1/x)/(1/(2x)+1/4)#?
• What is the quotient of #-18x^-2+27x^-2-72x^-8# and 9x?
• How do you simplify #(c^2/d)/(c^3/d^2)#?
• How do you simplify #((5g^3)/h^2)/((6g)/(5h))#?
• How do you simplify #(2/b)/(4/(b-3))#?
• How do you divide #(a+3)/(a^2+a-12)div (a^2-9)/(a^2+7a+12)#?
• How do you divide #(4k^2-29k-24)/(k^2-13k+40)# by #(4k^2+15k+9)/(5k^3-25k^2-3k+15)#?
• What is the remainder when #1 + x + x^2 + x^3 + ... + x^2006# is divided by #(x-1)# ?
• Let #h(x)=6x^5-5x^4+4x^3-3x^2-2x+x+7# and #m(x)=x^2-1#, how do you find the quotient h(x) and m(x)?
• How do you simplify #((2x-5)/(x^2-9))/((3x-1)/(x+3))#?
• How do you simplify #((3x-2)/(x^2-4))/((5x+1)/(x^2+x-6))#?
• How do you simplify #((x)/(x+1))/(x+x/3)#?
• How do you divide #\frac { 2x ^ { 1/ 8} } { x ^ { - 1/ 3} }#?
• How do you simplify #\frac { x ^ { 3} - 4x } { x ^ { 2} + x - 2}#?
• How do you divide #x^5+x^3+x# by #x^2+x+1# ?
• How do you solve #(5x)/2 - x = x/14 + 9/7#?
• Question #f78ff
• Simplify #(x^2-x)/(x-1)#?
• Question #33e19
• Question #a2631
• # ((a^2+ax+x^2)/(ax+2ay)) ÷( (a^3−x^3)/(bx+2by))# ?
• Given #p+q+r=0#, how do you prove that: #1/(1+x^p+x^(-q))+1/(1+x^q+x^(-r))+1/(1+x^r+x^(-p)) = 1# ?
• How do you simplify #\frac { 3m \cdot 7m } { 3m ^ { 0} }#?
• Question #52965
• Question #1125a
• How do you simplify #\frac { 16a b } { 56b c }#?
• How do you simplify #\frac { 3x ^ { 3} y ^ { 2} } { 2x ^ { 2} y ^ { 3} }#?
• How do you simplify #\frac { 20p ^ { 6} + 5p ^ { 4} } { 5p }#?
• How do you simplify #\frac { 2x ^ { 3} + 9x ^ { 2} y + 4x y ^ { 2} } { x ^ { 2} + 4x y }#?
• #(x-6) -: (6-x)#. Solve the rational expression?