How do you prove tan theta cot theta=1?

2 Answers
Alan P. · Kevin B.
Jun 8, 2015

By definition cot(theta) = 1/(tan(theta))

Explanation:

tan(theta) * cot(theta)

color(white)("XXXX")= tan(theta) * 1/tan(theta)

color(white)("XXXX")= cancel(tan(theta))* 1/cancel(tan(theta))

color(white)("XXXX")=1

Arunraju Naspuri · Stefan V.
Jun 9, 2015

We can prove it by right angle triangle.

Explanation:

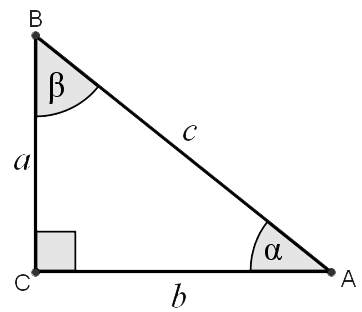
![http://www.mathportal.org/calculators/plane-geometry-calculators/http://right-triangle-calculator.php](https://useruploads.socratic.org/enqJSZMS6yK8CLpGBlRq_triangleRightAngle.gif)

tan( α )=a/b

cot(α )=b/a;

LHS=tan(alpha)xxcot(alpha)

=a/bxxb/a

=(cancela)/cancel(b)xx(cancel(b)/cancel(a))

=1

=RHS

Related questions
See all questions in Proving Identities
Impact of this question
32701 views around the world
You can reuse this answer
Creative Commons License