How do I us the Limit definition of derivative on #f(x)=e^x#?
1 Answer
The limit definition of the derivative is:
#d/dx f(x) = lim_(h->0) (f(x+h) - f(x))/h#
Now, since our function
#d/dx[e^x] = lim_(h->0) (e^(x+h) - e^x)/h#
At first, it may be unclear as to how we will evaluate this limit. We will first rewrite it a bit, using a basic exponent law:
#d/dx[e^x] = lim_(h->0) (e^(x) * e^h - e^x)/h#
And now, we will factor the
#d/dx[e^x] = lim_(h->0) (e^x (e^h - 1))/h#
It might not be obvious, but using the constant law of limits we can actually treat
#d/dx[e^x] = e^x * lim_(h->0) (e^h - 1)/h#
And now, the entire thing has been simplified a great deal. The tricky part is figuring out this last limit.
Since it's easier, we will attempt to evaluate the limit graphically. So let's take a look at a graph of the function
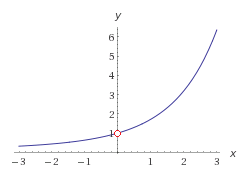
The "hole" at
And, we can observe this same trend when approaching from the negative side:
So, we can say with reasonable certainty that
Granted, one shouldn't assume that they will get the correct answer from evaluating a limit graphically. So, since I like certainty, and since there is a way to evaluate the above limit algebraically, I will explain the alternate method:
#lim_(h->0) (e^h - 1)/h#
Now, there are actually a few ways to define
#e = lim_(h->0) (1 + h)^(1/h)#
Since our previous limit also has the variable
#lim_(h->0) (((1 + h)^(1/h))^h - 1)/h#
Simplifying the inside gives:
#lim_(h->0) (1 + h - 1)/h#
This further simplifies to:
#lim_(h->0) h/h#
We can easily see that this limit evaluates to
So now that we know what this limit is, we can look back at our definition for the derivative of
#d/dx[e^x] = e^x * lim_(h->0) (e^h - 1)/h#
# = e^x * 1#
#= e^x#


