Question #0cdf5
2 Answers
(b) is 12.9s (c) is 66.2m/s and (d) is 24.2s (total time)
Explanation:
The question tells us that the car reaches 60mph from rest after 5.2s, hence the driver will be accelerating for this time (5.2s).
At this point it is useful to covert this speed into SI units:
So acceleration =
Whilst decelerating from the top speed to rest we are told that
For both phases of travel we can use
We can define the distance whilst accelerating as
When accelerating from rest:
And when decelerating to rest:
Since final velocity for accelerating phase (
And we also know that
Solving:
For (b) we can now use
For (c) top speed is given by
For (d), the time decelerating we can use
So total time =
-
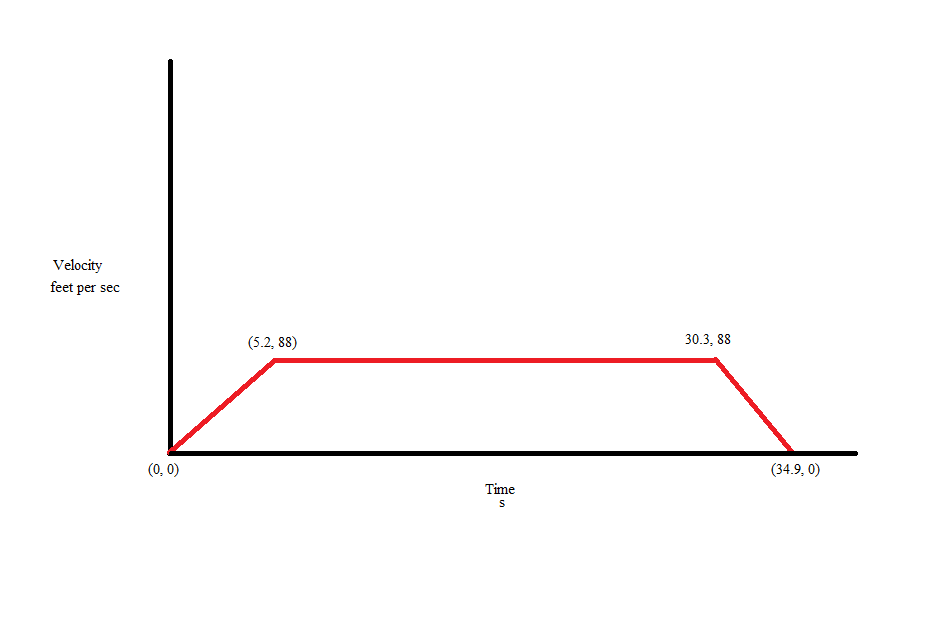
First step: Acceleration for the car is given for speed from
#0" to "60 mph# . It is assumed that it can not go above this maximum speed.
Let us assume that the driver initially accelerates the car for achieving maximum speed. Converting mph to fps#60mph=(60xx1760xx3)/3600=88fts^-1# and taking#g=32fts^-2# (all quantities rounded to one place of decimal).
Acceleration of the car during this period
#v=u+at#
#88=0+axx5.2#
#a=88/5.2fts^-2#
Distance moved during this acceleration period
#s_a=ut+1/2at^2#
#s_a=1/2xx88/5.2xx(5.2)^2#
#s_a=228.8ft# -
Second step: Test run is given as half mile. Balance distance of test run
#s_b=2640-228.8=2411.2ft#
Deceleration is given as#0.6g=0.6xx32=19.2ft s^-2#
Suppose the car is retarded as given and comes to halt. Using the kinematic equation the distance moved#s_d# is
#v^2-u^2=2as#
#0^2-88^2=2xx(-19.2)xxs_d#
#s_d=88^2/(2xx19.2)=201.7ft#
Time taken for this part of test run
#v=u+at#
#0=88+(-19.2)xxt_d#
#=>t_d=88/19.2=4.6s# - We see that there is still some distance to be covered for the test run. This distance
#s_t# needs to be covered at the top speed. We know that
#s_t=s_b-201.7=2411.2-201.7=2209.5ft#
Time taken to cover this distance#=2209.5/88=25.1s#
(a)
(b)
(c)
(d) Time of test run

