Question #45e44
1 Answer
Explanation:
The first thing to do here is use the molarity and volume of the initial solution to determine how many moles of solute, which in your case is potassium iodide,
#color(purple)(|bar(ul(color(white)(a/a)color(black)(c = n_"solute"/V_"solution" implies n_"solute" = c * V_"solution")color(white)(a/a)|)))#
You will have
#n_("KI initial") = "5.00 mol" * color(red)(cancel(color(black)("L"^(-1)))) * overbrace(50.0 * 10^(-3)color(red)(cancel(color(black)("L"))))^(color(blue)("volume in liters"))#
#n_("KI initial") = "0.250 moles KI"#
Now, you know that
#3.05 color(red)(cancel(color(black)("g"))) * "1 mole KI"/(166.003 color(red)(cancel(color(black)("g")))) = "0.01837 moles KI"#
Use the known volume of the dilute solution to figure out its molarity. Since
#c_"diluted" = "0.01837 moles"/(25.0 * 10^(-3)"L") = "0.7348 M"#
You now know that the initial solution must be diluted to a final concentration of
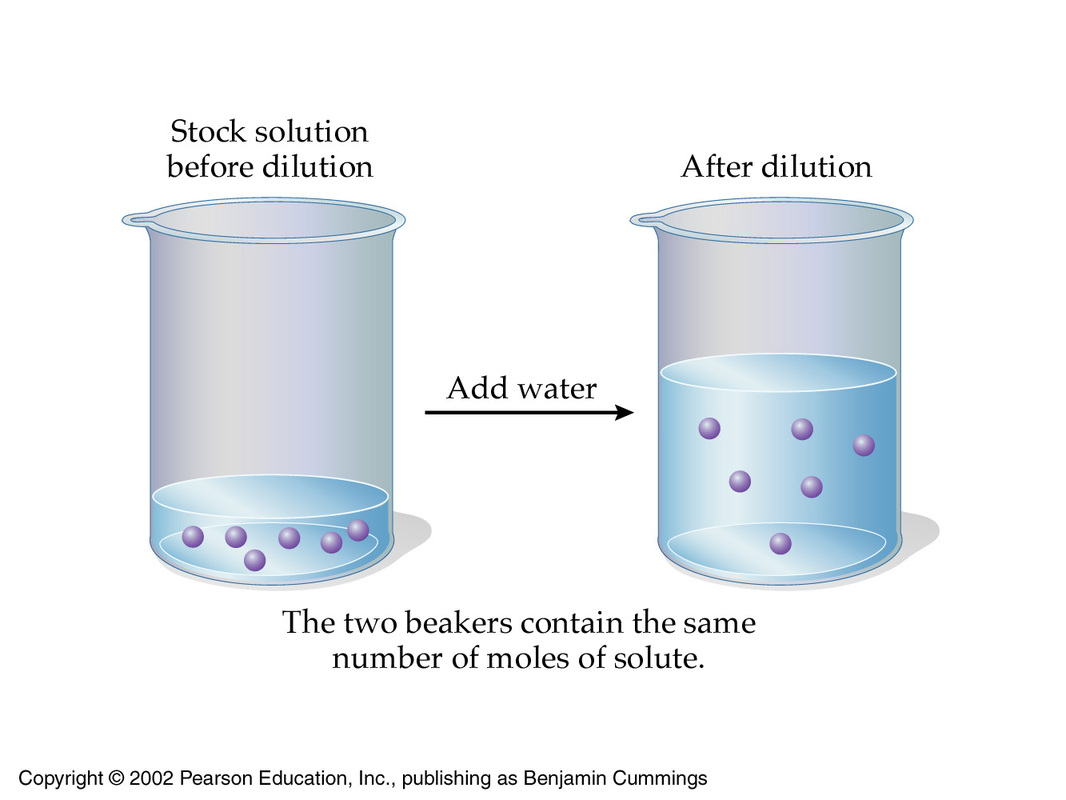
The equation for dilution calculations looks like this
#color(blue)(overbrace(c_1 xx V_1)^(color(darkgreen)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(darkgreen)("moles of solute in diluted solution"))#
Here
Rearrange to solve for
#c_1 * V_1 = c_2 * V_2 implies V_2 = c_1/c_2 * V_1#
Plug in your values to find
#V_2 = (5.00 color(red)(cancel(color(black)("M"))))/(0.7348color(red)(cancel(color(black)("M")))) * "50.0 mL" = "340.22 mL"#
Rounded to three sig figs, the answer will be
#V_2 = color(green)(|bar(ul(color(white)(a/a)color(black)("340. mL")color(white)(a/a)|)))#
So, you know that if you start with

