#intx -csc(x) dx#
#=int x dx - int csc(x) dx#
#=(x^2)/2-ln(abs(csc(x) - cot(x))) + C#
Where #C# is a constant of integration.
So #f(x) = (x^2)/2-ln(abs(csc(x) - cot(x))) + C#
Using the fact that #f((5pi)/4) = 0 #, we can substitute:
#f((5pi)/4)=(((5pi)/4)^2)/2-ln(abs(csc((5pi)/4) - cot((5pi)/4))) + C#
Moreover,
#(((5pi)/4)^2)/2-ln(abs(csc((5pi)/4) - cot((5pi)/4))) + C = 0#
Simplifying, we get
#(25pi^2)/32-ln(abs(-sqrt(2)-1))+C=0#
#(25pi^2)/32-ln(sqrt(2)+1)+C=0#
#C=ln(sqrt(2)+1)-(25pi^2)/32#
Therefore, the answer is:
#f(x) = (x^2)/2-ln(abs(csc(x) - cot(x))) + ln(sqrt(2)+1)-(25pi^2)/32#
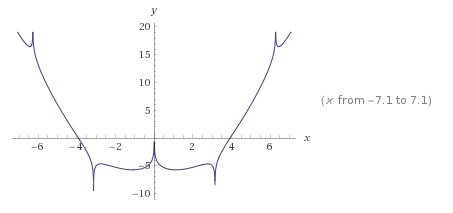
Here's an image of what the graph looks like:
 )
)
 )
) 