Here's a useful diagram that shows the relation between the three quantities.
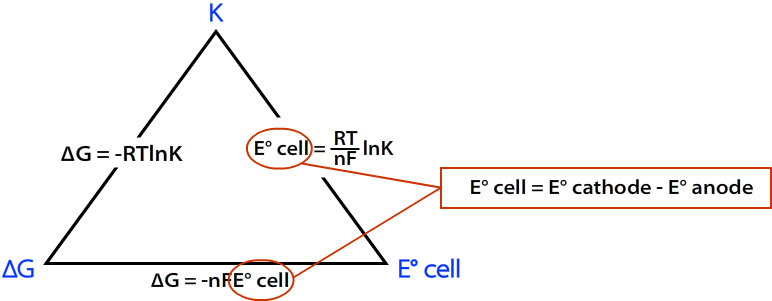
Calculate the standard cell potential
#color(white)(mmmmmmmmmmmmmmmmmmmmll)E^@"/V"#
#3/2×["2H"^"+""(aq)" + "2e"^"-" → "H"_2"(g)"]color(white)(mmmmmml)0.00#
#ul(1 ×["Al(s)" + "3e"^"-" → "Al"^"3+""(aq)"])color(white)(mmmmmm)ul("+1.66")#
#"Al(s)" + "3H"^"+""(aq)" → "Al"^"3+""(aq)" + 3/2"H"_2"(g)"color(white)(mll)"+1.66"#
Calculate #ΔG^@#
#ΔG^@ = "-"nFE_text(cell)^@ = "-3" × "96 485 J"·color(red)(cancel(color(black)("V")))^"-1""mol"^"-1" × 1.66 color(red)(cancel(color(black)("V"))) = "-480 000 J·mol"^"-1" = "-480 kJ·mol"^"-1"#
Calculate #K#
#E^@ = (RT)/(nF)lnK#
#lnK = (nFE^@)/(RT) = (3 × "96 485" color(red)(cancel(color(black)("J·V"^"-1""mol"^"-1"))) × 1.66 color(red)(cancel(color(black)("V"))))/(8.314 color(red)(cancel(color(black)("J·K"^"-1""mol"^"-1")))× 298 color(red)(cancel(color(black)("K")))) = 194#
#K = e^194 = 2× 10^84#
That's a BIG equilibrium constant.

