Because there exist exactly three p orbitals per quantum level n, and because the (n-1)d orbital is closer in energy to the (n-1)s orbital than an np orbital.
It sounds like a misunderstanding of the hybridization notation.
HYBRIDIZATION NOTATION
Having sp^3 hybridization tells you that one ns orbital mixes with three np orbitals to generate four identical (in symmetry), degenerate (in energy) sp^3 orbitals. That way, the given compound can form up to four identical bonds if it wishes.
From the explanation above, using n = 4, it follows that sp^4 implies the existence of a fourth (n-1)p orbital, or implies an np orbital somehow participates as the fourth p orbital.
However, that is not reasonable, given that an np orbital is too far away in energy to interact in place of using the (n-1)d orbital for n = 4. Furthermore, there exist only three (n-1)p orbitals, not four---remember that for l = 1 (for all p orbitals), m_l = {-1,0,+1}.
A MORE EXPLICIT EXAMPLE
The 3d orbital, for instance, is closer in energy to the 3s orbital than the 4p is to the 3s for a given atom.
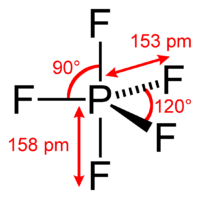
That means it is more favorable to mix one 3s, three 3p, and one 3d if the compound wishes to form five bonds using sp^3d hybridization.
An example of sp^3d would be PF_5.
useruploads.socratic.org)
