What is the frequency of limiting line in Balmer series?

Question

35474 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-05T02:29:38

$f = 8.225 \times 10^{14} l Hz$ $f = 8.225 × 10^14color(white)(l)"Hz"$

The Balmer series corresponds to all electron transitions from a higher energy level to $n = 2$ $n = 2$ .

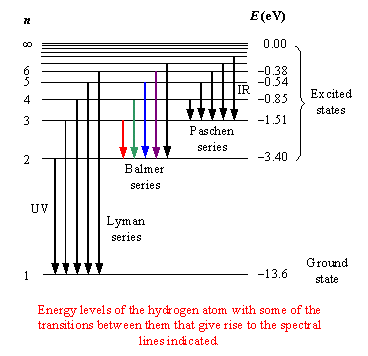
eilat.sci.brooklyn.cuny.edu

The wavelength is given by the Rydberg formula

$color(blue)(bar(ul(|color(white)(a/a) 1/λ = R(1/n_1^2 -1/n_2^2)color(white)(a/a)|)))" "$

where

$R =$ the Rydberg constant and
$n_1$ and $n_2$ are the energy levels such that $n_2 > n_1$

Since $fλ = c$

we can re-write the equation as

$1/λ = f/c = R(1/n_1^2 -1/n_2^2)$

or

$f = cR(1/n_1^2 -1/n_2^2) = R^'(1/n_1^2 -1/n_2^2)$

where $R^'$ is the Rydberg constant expressed in energy units ( $3.290 × 10^15 color(white)(l)"Hz"$ ).

In this problem, $n_1 = 2$ , and the frequency of the limiting line is reached
as $n → ∞$ .

Thus,

$f = lim_(n → ∞)R^'(1/4 -1/n_2^2) = R^'(0.25 - 0) = 0.25R^'$

$= 0.25 × 3.290 × 10^15 color(white)(l)"Hz" = 8.225 × 10^14color(white)(l)"Hz"$