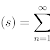What is the distance between the following polar coordinates?: # (3,(-7pi)/12), (2,(7pi)/8) #
1 Answer
May 14, 2018
Explanation:
Say you have two polar coordinates
To find our distance we just then have: