The base of a triangular pyramid is a triangle with corners at (7 ,6 ), (4 ,3 ), and (1 ,8 ). If the pyramid has a height of 6 , what is the pyramid's volume?

1 Answer
Jan 4, 2018

The volume of the pyramid is 24.

Explanation:

Let A=(7,6),B=(4,3),C=(1,8)

When we need to calculate area of an arbitrary triangle with integer coordinates of vertices, it could be useful to draw it and then a rectangle around it. The rectangle should have sides parallel to axes.

![https://www.geogebra.org/geometry]
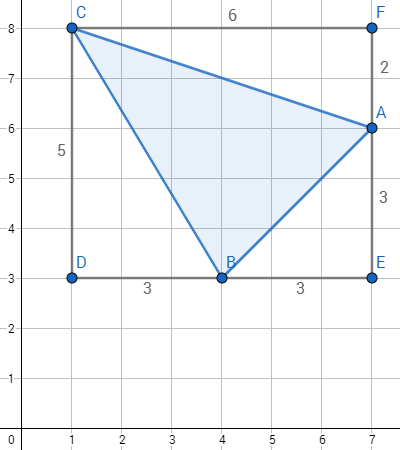(useruploads.socratic.org)

Now we can calculate area of the rectangle and subtract areas of white right triangles. It's much easier than calculating blue triangle's area directly.
[XYZ] is the area of shape XYZ.

So
[ABC]=[CDEF]-([BCD]+[ABE]+[ACF])
[ABC]=6*5-(1/2*3*5+1/2*3*3+1/2*6*2)
[ABC]=30-1/2(15+9+12)
[ABC]=30-36/2=30-18=12

Now we have base area P=12 and height h=6 and we can calculate volume of the pytamid by the formula
V=1/3*P*h=1/3*12*6=24

Related questions
See all questions in Volume of Solids
Impact of this question
1977 views around the world
You can reuse this answer
Creative Commons License