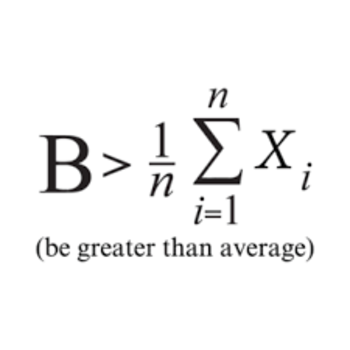How to use the discriminant to find out how many real number roots an equation has for 2m^2 - m - 6 = 0?

1 Answer
Oliver S.
Mar 26, 2018

See answer

Explanation:

The discriminant, (Delta), is derived from quadratic equation:
x=(b^2+-(sqrt(b^2-4ac)))/(2a)

Where Delta is the expression beneath the root sign, hence:
The discriminant (Delta) =b^2-4ac

If Delta>0 there are 2 real solutions (roots)
If Delta=0 there is 1 repeated solution (root)
If 0>Delta then the equations has no real solutions (roots)

In this case b=-1, c=-6 and a=2
b^2-4ac=(-1)^2-4(2)(-6)=49

So your equation has two real solutions as Delta>0. Using the quadratic formula these turn out to be:

x=(1+-(sqrt49))/(4)

x_1=2

x_2=(-6/4)=-1.5

Related questions
See all questions in Solutions Using the Discriminant
Impact of this question
1911 views around the world
You can reuse this answer
Creative Commons License