How solve it? Topic: DERIVATE
Please I need help I do not know how to solve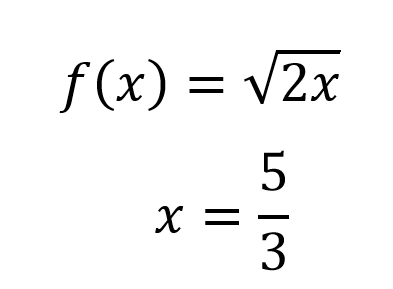
Please I need help I do not know how to solve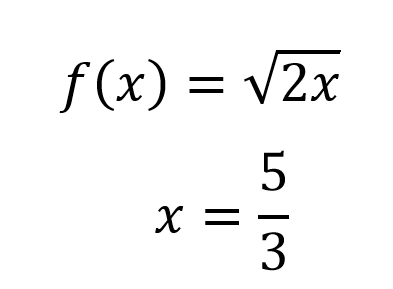
2 Answers
#f(x)=sqrt(2x)#
First, let's rewrite the square root as a
#f(x)=(2x)^(1/2)#
Now, we need to recognize that these can be split up as a constant and a variable function.
#f(x)=2^(1/2)*x^(1/2)#
When we differentiate, multiplicative constants like the
To differentiate
Then, we see that:
#f'(x)=2^(1/2)*(1/2x^(1/2-1))#
Now simplifying:
#f'(x)=2^(1/2)/2x^(-1/2)#
#f'(x)=1/(2^(1/2)*x^(1/2))#
#f'(x)=1/sqrt(2x)#
So at
#f'(5/3)=1/sqrt(2*5/3)=1/sqrt(10/3)=sqrt(3/10)#
Explanation:
show below:
The derivative at


