How do you use pascals triangle to expand #(d + 5)^7#?

1 Answer
Noah G
Jul 31, 2016

Here is Pascal's Triangle:

http://mathforum.org/workshops/usi/pascal/mo.pascal.html

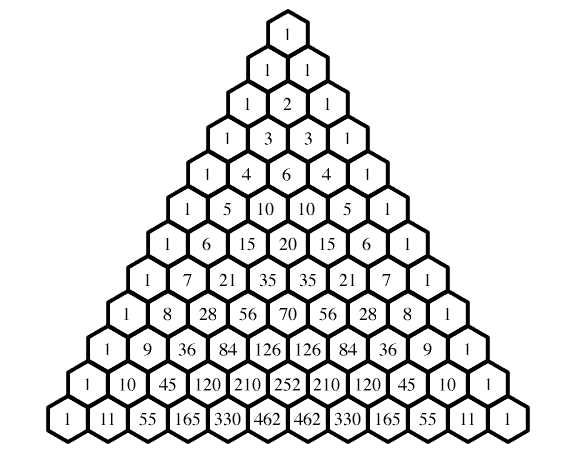
What do you notice?

You probably see that each number going down, after the first row, is the sum of the two numbers directly above it.

If you're extremely perceptive, you'll also notice that the sum of each row is given by #2^(n - 1) #, where n is the row number.

Now back to our problem at hand. The first thing we must do is determine the number of terms in our expansion. There are always #n + 1# terms in the expansion of #(x + y)^n#, so there will be #8# terms in this expansion. Now, we need to find the row in Pascal's Triangle that has #8# terms. That is the row with numbers #"1-7-21-35-35-21-7-1"#.

Multiply this with descending exponents on the #d# term and increasing exponents on the #5#:

#(d + 5)^7 = 1 xx d^7 xx 5^0 + 7 xx d^6 xx 5^1 + 21 xx d^5 xx 5^2 + 35 xx d^4 xx 5^3 + 35 xx d^3 xx 5^4 + 21 xx d^2 xx 5^5 + 7 xx d^1 xx 5^6 + 1 xx d^0 xx 5^7#

#(d + 5)^7 = d^7 + 35d^6 + 525d^5 + 4375d^4 + 21875d^3 + 65625d^2 + 109375d + 78125#

There's your expansion!

Hopefully this helps!

Related questions
See all questions in Pascal's Triangle and Binomial Expansion
Impact of this question
4724 views around the world
You can reuse this answer
Creative Commons License