 )
)
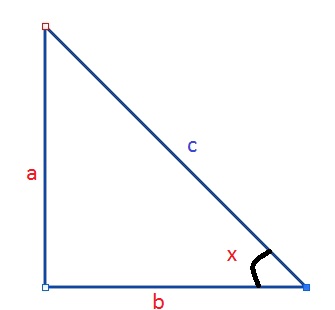
#cosx=b/c##" "color(blue)((1))#
#sinx=a/c##" "color(blue)((2))#
Given that,
#sinx+cosx=sqrt2##" "color(blue)((3))#
Substitute #" "color(blue)((1))# and #color(blue)((2))# in #" "color(blue)((3))#
#a/c+b/c=sqrt2##=>(a+b)/c=sqrt2#
#a+b=csqrt2#
squaring on both sides
#(a+b)^2=(csqrt(2))^2##=>(a+b)^2=2c^2#
#a^2+b^2+2ab=2c^2#
#c^2+2ab=2c^2#[since from Pythagoras]
#c^2=2ab#
#a^2+b^2=2ab#[since from Pythagoras]
#a^2+b^2-2ab=0#
#(a-b)^2=0#
#a-b=0#
#a=b##" "color(blue)((4))#
equation#" "color(blue)((4))# substitute in#" "color(blue)((1))#
#cos x=a/c##" "color(blue)((5))#
From#" "color(blue)((5))#&#" "color(blue)((2))#
#cosx=sinx#
#sin(pi/2-x)=sinx#
#cancel(sin)(pi/2-x)=cancel(sin)x#
#pi/2-x=x##=>2x=pi/2#
#x=pi/4#radians
or
#x=45^@#
 )
)  )
)