Given: #8=(3x-y)^2+2y+6x#
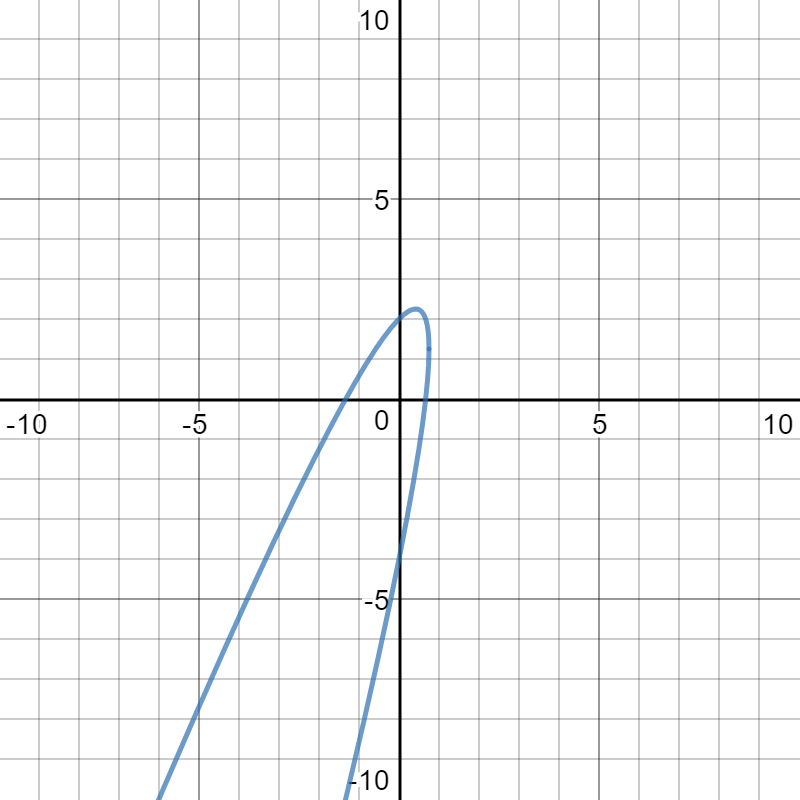
Here is a graph of the Cartesian equation:
 )
)
Expand the square:
#9x^2-6xy+y^2+6x+2y-8 = 0#
Substitute #rcos(theta)# for every x:
#9(rcos(theta))^2-6(rcos(theta))y+y^2+6(rcos(theta))+2y-8 = 0#
Substitute #rsin(theta)# for every y:
#9(rcos(theta))^2-6(rcos(theta))(rsin(theta))+(rsin(theta))^2+6(rcos(theta))+2(rsin(theta))-8 = 0#
There is a common factor of #r^2# in the first 3 terms:
#(9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta))r^2+6(rcos(theta))+2(rsin(theta))-8 = 0#
There is a common factor of r in the next 2 terms:
#(9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta))r^2+(6cos(theta)+2sin(theta))r-8 = 0#
The above is a quadratic equation in standard form where:
r in the independent variable
#a = 9cos^2(theta)-6cos(theta)sin(theta)+sin^2(theta)#
#b = 6cos(theta)+2sin(theta)#
#c = -8#
We use the identity #cos^2(theta) + sin^2(theta) = 1 to simplify a:
#a = 8cos^2(theta)-6cos(theta)sin(theta)+1#
We can use the quadratic formula to write r and a function of #theta# but, because radii should only be positive we will discard the negative root:
#r = (-b+sqrt(b^2-4(a)(c)))/(2a)#
Substitute for every a:
#r = (-b+sqrt(b^2-4(8cos^2(theta)-6cos(theta)sin(theta)+1)(c)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))#
Substitute for c:
#r = (-b+sqrt(b^2+32(8cos^2(theta)-6cos(theta)sin(theta)+1)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))#
Substitute for every b:
#r = (-(6cos(theta)+2sin(theta))+sqrt((6cos(theta)+2sin(theta))^2+32(8cos^2(theta)-6cos(theta)sin(theta)+1)))/(2(8cos^2(theta)-6cos(theta)sin(theta)+1))#
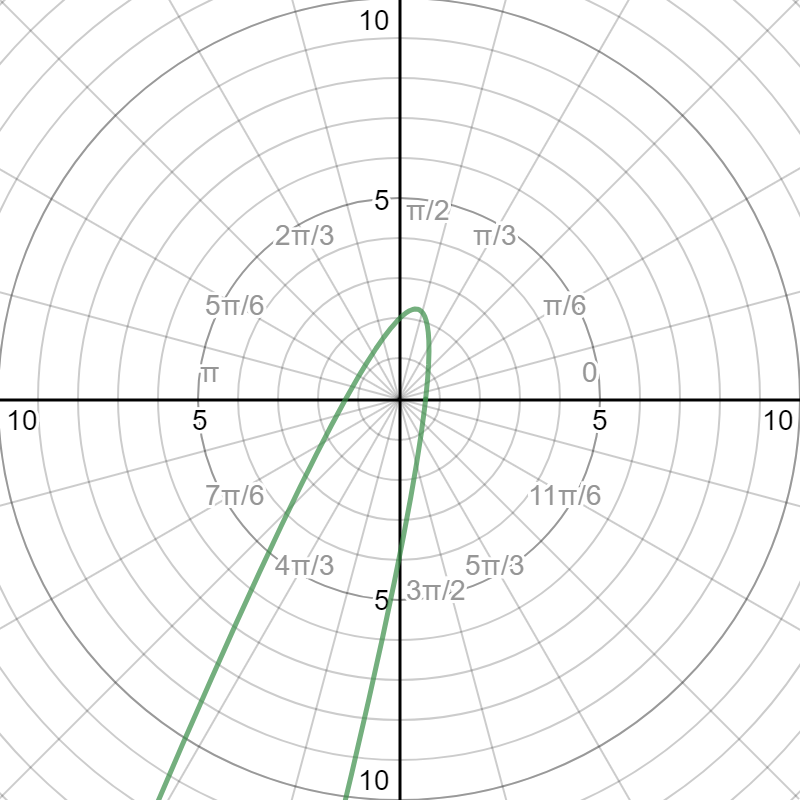
Here is a graph of the polar equation:
 )
)
The graphs are identical, therefore, the conversion is complete.
Note: I am sure that the expression under the radical can be simplified but I will leave that to you.
 )
)  )
) 