An electron is in the hydrogen atom with `n = 3`. `|L| = sqrt6 ℏ` . Which is a possible angle between `vecL` and the `z` axis?

In the Schrödinger equation for the hydrogen atom, the squared orbital angular momentum operator, `hatL^2`, corresponds to the eigenvalue, `l(l+1)ℏ^2`, according to this formula:

`bar(ul(|color(white)(a/a) ul(hat(L)^2)Y_(l)^(m_l)(theta,phi) = ul(l(l+1)ℏ^2)Y_(l)^(m_l)(theta,phi) color(white)(a/a)|))" "`

or

`color(blue)(bar(ul(|color(white)(a/a) ul(hat(L)) harr ul(sqrt(l(l+1))ℏ) color(white)(a/a)|)))" "`

where

• `l` is the angular momentum quantum number.
• `Y_(l)^(m_l)(theta,phi)` is the spherical harmonic wave function for the orbital of a given `l` and `m_l`.
• `m_l` is the magnetic quantum number, and the projection of `l` along the `z` axis.

The `z`-component of the angular momentum similarly corresponds to the eigenvalue `m_lℏ` according to:

`bar(ul(|color(white)(a/a)ul(hatL_z)Y_(l)^(m_l)(theta,phi) = ul(m_lℏ)Y_(l)^(m_l)(theta,phi)color(white)(a/a)|))" "`

or

`color(blue)(bar(ul(|color(white)(a/a)ul(hatL_z) harr ul(m_lℏ) harr |L|cosθcolor(white)(a/a)|)))" "`

where

• `m_l` is the magnetic quantum number and
• `θ` is the angle that `vecL` makes with the `z`-axis, or the angle of `hatL` with respect to `m_l`.

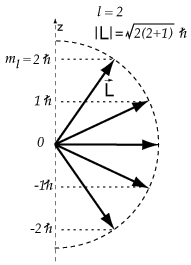
Thus

`θ = cos^"-1"(m_l/|L|)`

Some possibilities for `n = 3` are

`bb(lcolor(white)(mmm)|L|//ℏ)`
`0color(white)(ml)sqrt(0(1)) = 0`
`1color(white)(ml)sqrt(1(2)) = sqrt2`
`2color(white)(ml)sqrt(2(3)) = sqrt6`

It appears that our electron is a `"d"` electron (`l = 2`).

and

`|L| = sqrt6ℏ = 2.4495ℏ`

The possible angles for a `"d"` electron are

`bb(color(white)(m)|L|"/"ℏcolor(white)(mm)m_l//ℏcolor(white)(ml)cosθcolor(white)(mmm)θ)`

`2.4495 color(white)(mml)2color(white)(mml)0.8165color(white)(mll)35.26`
`2.4495 color(white)(mml)1color(white)(mml)0.4082color(white)(mll)65.90`
`2.4495 color(white)(mml)0color(white)(mml)0color(white)(mmmml)90`
`2.4495 color(white)(mm)"-1"color(white)(mm)"-0.4082"color(white)(m)114.09`
`2.4495 color(white)(mm)"-2"color(white)(mm)"-0.8165"color(white)(m)144.74`

The only angle that agrees with those given in the question is 65.90°.