Here is Pascal's Triangle:
 )
)
Here is the same triangle but in the context of binomial expansion:
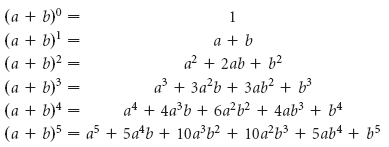
In the expression #(2+5i)^4#, our #a# is #2# and our #b# is #5i#. Now, we use the fourth row in the second picture and plug in our values (I color-coded each part so it is easier to follow):
#color(white)=>color(red)(a^4)+color(orange)(4a^3b)+color(green)(6a^2b^2)+color(blue)(4ab^3+b^4)#
#=>color(red)((2)^4)+color(orange)(4(2)^3(5i))+color(green)(6(2)^2(5i)^2)+color(blue)(4(2)(5i)^3)+color(purple)((5i)^4)#
#=color(red)16+color(orange)(4*8*5i)+color(green)(6*4*5^2*i^2)+color(blue)(4*2*5^3*i^3)+color(purple)(5^4*i^4)#
#=color(red)16+color(orange)(160i)+color(green)(600*i^2)+color(blue)(1000*i^2*i)+color(purple)(625*(i^2)^2)#
#=color(red)16+color(orange)(160i)+color(green)(600*-1)+color(blue)(1000*-1*i)+color(purple)(625*(-1)^2)#
#=color(red)16+color(orange)(160i)color(green)(-600)color(blue)(-1000i)+color(purple)(625*1)#
#=color(red)16color(green)(-600)+color(purple)(625)+color(orange)(160i)color(blue)(-1000i)#
#=41+color(orange)(160i)color(blue)(-1000i)#
#=41-840i#
That's the result!
 )
)
