Due to the request for clarification in the question, this answer is a bit long. Feel free to skip over any unneeded explanations.
Unless otherwise specified, we generally consider the argument of a trigonometric function to be in radians. Radians are, in a sense, the natural way of measuring an angle within a circle, as they relate the radius of the circle to the angle measured (one radian is the measure of an angle subtended by an arc whose length equals the radius). A full circle is #2pi# radians (equivalent to #360^@#), and as such, #pi# appears quite commonly in well known angles.
With that in mind, let's see what this problem is asking.
 )
)
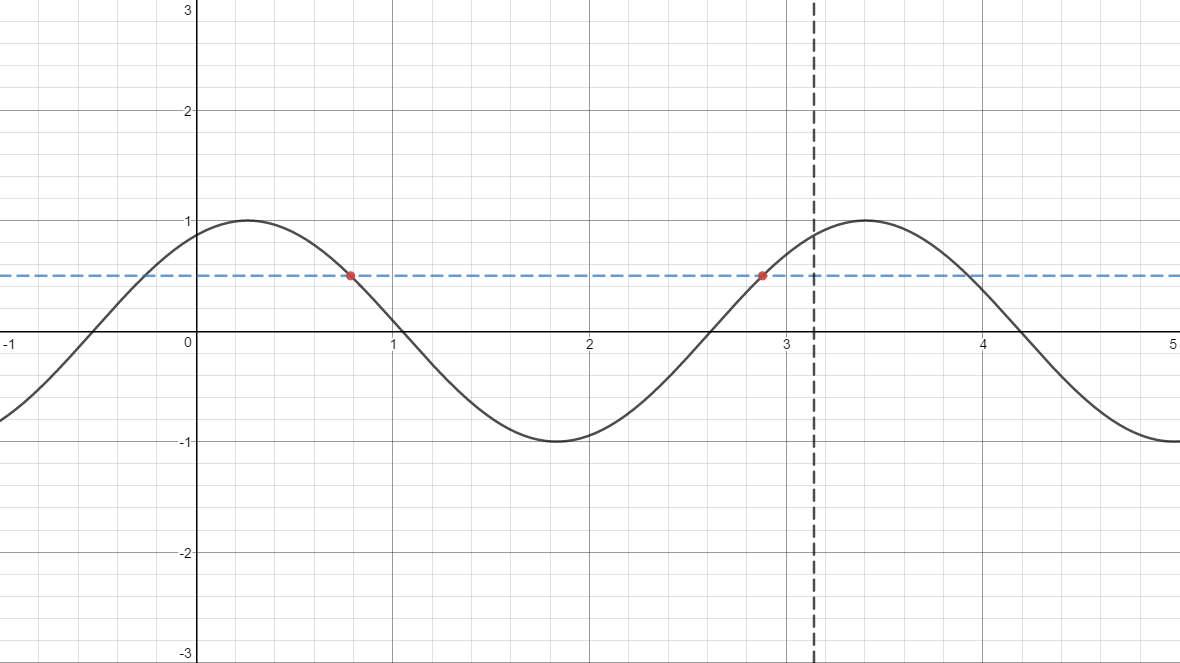
The above is a graph of #y = sin(2x+pi/3)#, with dashed lines showing #y=1/2# and #x=pi#. Note that between #x=0# and #x=pi#, the #y=1/2# line intersects our graph at two points. The #x#-coordinates of those points are our solutions.
To figure out what those points are, we will consult the unit circle .
 )
)
On the unit circle, the #x# and #y# coordinates tell us the value of #cos(theta)# and #sin(theta)#, respectively. For example, from the circle, we see that #sin(theta) = 1/2# at #theta = pi/6# and #theta = (5pi)/6#.
(The angles shown on the circle and the values of sine and cosine at those angles are good to have memorized. As a side note, they can be derived by using the sohcahtoa definition on the special right triangles with angles #30^@-60^@-90^@# or #45^@-45^@-90^@#. Additionally, because it is a circle, we can add or subtract any multiple of #2pi# (#360^@#) to an angle without changing the values of the trig functions.)
From the above, we now know that for #sin(x)# to equal #1/2#, we need #x = pi/6 + 2pik# or #x = (5pi)/6+2pik# where #k# is an integer. We can now solve the problem algebraically. Substituting our argument #2theta+pi/3# for #x#, we get
#2theta+pi/3 = pi/6 + 2pik#
#=> 2theta = -pi/6+2pik#
#=> theta = -pi/12 + pik#
OR
#2theta+pi/3 = (5pi)/6+2pik#
#=> 2theta = pi/2 + 2pik#
#=> theta = pi/4+pik#
Now we consider the restriction #0 <= theta <= pi# to see what integers we can use for #k#. To get #theta# to stay within that range, we must have #k=1# for the first possibility, and #k = 0# for the second. Thus, we get two answers:
#theta = -pi/12 + 1pi = (11pi)/12#
OR
#theta = pi/4 + 0pi = pi/4#
Thus, we have the solution set #theta in {pi/4, (11pi)/12}#.
Checking, we find that the equality hold for each of the above values:
#sin(2(pi/4)+pi/3) = sin(pi/2+pi/3) = sin((5pi)/6) = 1/2#
#sin(2((11pi)/12)+pi/3) = sin((11pi)/6+pi/3) = sin(pi/6+2pi) = 1/2#
 )
)  )
)

