Using Right Riemann Sums, approximate the area under the curve #5x^2-4x# in the interval #[0,3]# with #6# strips?

1 Answer
Steve M
Jun 27, 2017

# 35.875 #

Explanation:

We have:

# f(x) = 5x^2-4x #

We want to calculate over the interval #[0,3]# with #6# strips; thus:

# Deltax = (3-0)/6 = 0.5#

Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

enter image source here

Right Riemann Sum

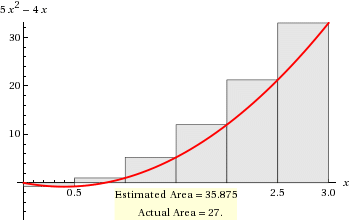
enter image source here

# R RS = sum_(r=1)^6 f(x_i)Deltax_i #
# " " = 0.5 * (-0.75 + 1 + 5.25 + 12 + 21.25 + 33) #
# " " = 0.5 * (71.75) #
# " " = 35.875 #

Actual Value

For comparison of accuracy:

# Area = int_0^3 \ 5x^2-4x \dx #
# " " = [(5x^3)/3-2x]_0^3 #
# " " = 45-6 #
# " " = 39 #

Related questions
See all questions in RAM (Rectangle Approximation Method/Riemann Sum)
Impact of this question
4854 views around the world
You can reuse this answer
Creative Commons License