The base of a triangular pyramid is a triangle with corners at #(7 ,6 )#, #(4 ,3 )#, and #(1 ,8 )#. If the pyramid has a height of #6 #, what is the pyramid's volume?

1 Answer
Jan 4, 2018

The volume of the pyramid is 24.

Explanation:

Let #A=(7,6),B=(4,3),C=(1,8)#

When we need to calculate area of an arbitrary triangle with integer coordinates of vertices, it could be useful to draw it and then a rectangle around it. The rectangle should have sides parallel to axes.

https://www.geogebra.org/geometry

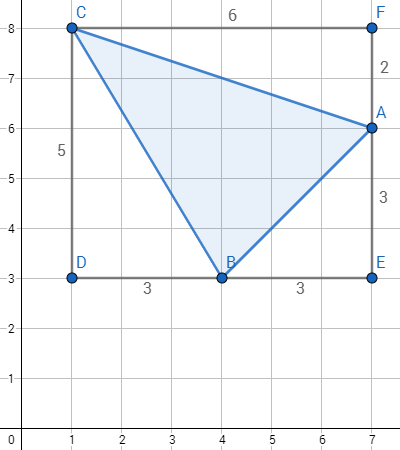Now we can calculate area of the rectangle and subtract areas of white right triangles. It's much easier than calculating blue triangle's area directly.
#[XYZ]# is the area of shape #XYZ#.

So
#[ABC]=[CDEF]-([BCD]+[ABE]+[ACF])#
#[ABC]=6*5-(1/2*3*5+1/2*3*3+1/2*6*2)#
#[ABC]=30-1/2(15+9+12)#
#[ABC]=30-36/2=30-18=12#

Now we have base area #P=12# and height #h=6# and we can calculate volume of the pytamid by the formula
#V=1/3*P*h=1/3*12*6=24#

Related questions
See all questions in Volume of Solids
Impact of this question
1737 views around the world
You can reuse this answer
Creative Commons License