What is the standard form of a polynomial #(5k + 2)(3k + 1)#?

Recall that the standard form of a polynomial is written in the form:

#color(teal)(|bar(ul(color(white)(a/a)ax^2+bx+c=0color(white)(a/a)|)))color(white)(X),color(white)(X)#where #a!=0#

For simplifying a quadratic equation into standard form, the F.O.I.L. (first, outside, inside, last) method is often used to expand the brackets. Here is what you will need to know before we start:

#1#. Assuming the given equation is equal to #0#, locate the terms, as well as their appropriate positive or negative signs.

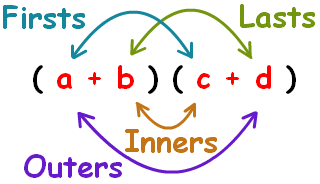
#(color(red)(5k)# #color(blue)(+2))(color(orange)(3k)# #color(green)(+1))=0#

#2#. For the "F" (first) in F.O.I.L., multiply #color(red)(5k)# and #color(orange)(3k)# together.

#color(red)(5k)(color(orange)(3k))#

#=color(purple)(15k^2)#

#3#. For the "O" (outside) in F.O.I.L., multiply #color(red)(+5k)# and #color(green)(1)# together.

#color(purple)(15k^2)# #color(red)(+5k)(color(green)1)#

#=color(purple)(15k^2)# #color(purple)(+5k)#

#4#. For the "I" (inside) in F.O.I.L., multiply #color(blue)(+2)# and #color(orange)(3k)# together.

#color(purple)(15k^2)# #color(purple)(+5k)# #color(blue)(+2)(color(orange)(3k))#

#=color(purple)(15k^2)# #color(purple)(+5k)# #color(purple)(+6k)#

#5#. For the "L" (last) in F.O.I.L., multiply #color(blue)(+2)# and #color(green)(1)# together.

#color(purple)(15k^2)# #color(purple)(+5k)# #color(purple)(+6k)# #color(blue)(+2)color(green)((1))#

#=color(purple)(15k^2)# #color(purple)(+5k)# #color(purple)(+6k)# #color(purple)(+2)#

#6#. Simplify the equation.

#color(green)(|bar(ul(color(white)(a/a)15k^2+11k+2=0color(white)(a/a)|)))#