What is the area of a triangle with sides of length 2, 4, and 5?

Question

4360 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-26T07:17:05

#color(blue)("Area of the triangle " A_t = 3.8 " sq units"#

#"Given : " a = 2, b = 4, c = 5#

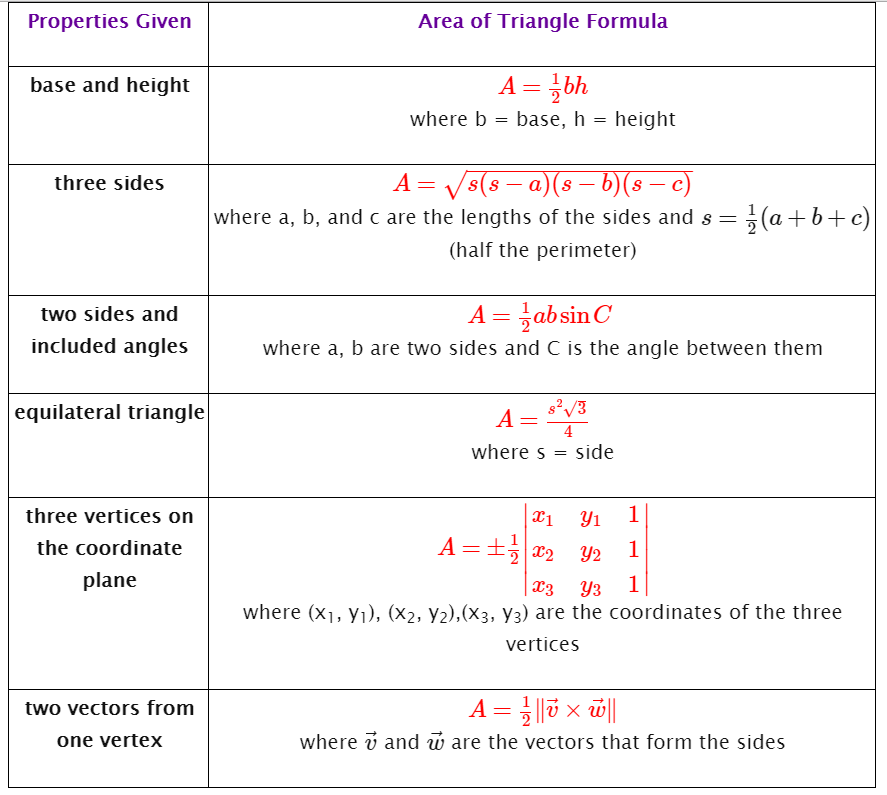
Having known three sides, we can calculate the area of the triangle using the formula,

#A_t = sqrt(s * (s-a) * (s-b) * (s-c))#

where s is the semi-perimeter of the triangle and a,b,c are the sides.

#s = (a + b + c) / 2 = (2 + 4 + 5) / 2 = 5.5#

#A_t = sqrt(5.5 * (5.5 - 2) * (5.5 - 4) * (5.5 - 5))#

#=> sqrt(5.5 * 3.5 * 1.5 * 0.5) ~~ 3.8 " sq units"#