Sketch the graph of #y= sin theta # for #-pi <= theta <=pi#?

Question

2082 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-20T15:17:16

See below.

To sketch this we must know 4 common points of the graph.

We know that #pi# in radians is #180^circ#

This means that #pi/2# is #90^circ#

From our knowledge, a sine graph has the coordinates:

#(0,0) (90,1) (180,0) ( -90, -1) (-180,0)#

Converting these to radians we get:

#(0,0) ( pi/2,1) (pi,0) ( -pi/2) ( -pi,0)#

We know that a sine graph oscillates between #1# and #-1#.

This means we need to label the #y# axis with the #1# and #-1#.

Along the #x# axis we must go up in radians, use the points mentioned above.

Plot the points on the graph and sketch with a nice smooth curve.

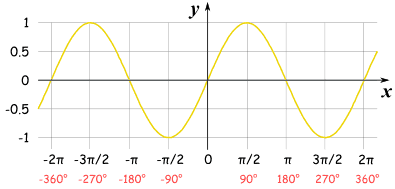
www.mathsisfun.com

Notice that the graph repeats this pattern throughout.