Schrödinger's wave equation gives which type of concept of quantum number?

The Schrodinger equation is constrained so that the energies that arise from solving it are all dependent in some way on quantum numbers, which are all integers (except for `m_s`, which is purely based on a property of a fermion).

EXAMPLE 1: PARTICLE IN A 3D BOX

For instance, for a system modeled as a three-dimensional particle in a box, the energy goes as

`E_n = (h^2)/(8m)(n_x^2/L_x^2 + n_y^2/L_y^2 + n_z^2/L_z^2)`,

`n_q = 1, 2, 3, . . .` is the principal quantum number for the `q`th dimension, and everything else is a constant.

![https://plus.maths.org/]()

EXAMPLE 2: HARMONIC OSCILLATOR

For a system modeled as a harmonic oscillator (ball and spring), the energy goes as

`E_(upsilon) = hnu(upsilon + 1/2)`,

`upsilon = 0, 1, 2, . . .` is the vibrational quantum number. `h` is Planck's constant in `"J"cdot"s"` and `nu` is the fundamental vibrational frequency in `"s"^(-1)`.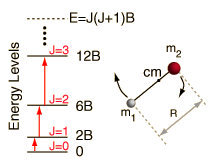

![)

EXAMPLE 3: DIATOMIC RIGID ROTATOR

For a system modeled as a diatomic rigid rotator (two balls connected by a stiff rod, rotating), the energy goes as

`E_J = J(J+1)B`,

`J = 0, 1, 2, . . .` is the rotational quantum number for a two-dimensional rigid rotator. Basically, `B` is the rotational constant, dependent on the identity of the molecule.


You can see that in all of these cases, in some way, the energy that arises from solving the Schrodinger equation is restricted to certain energy levels that are directly tied to the quantum number for that system.