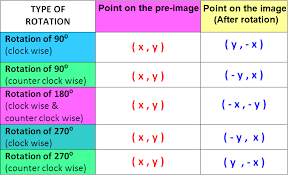
Point A is at #(8 ,-2 )# and point B is at #(5 ,-7 )#. Point A is rotated #(3pi)/2 # clockwise about the origin. What are the new coordinates of point A and by how much has the distance between points A and B changed?

1 Answer
sankarankalyanam
Mar 29, 2018

#color(purple)("Increase in distance due to rotation " = 10.72 " units"#

Explanation:

#"Coordinates of " A(8,-2), B (5, -7)#

#vec (AB) = sqrt((8-5)^2 + (-2+7)^2) = 5.83#

Point A rotated about the origin by #(3pi)/2# clockwise.

https://www.onlinemath4all.com/rotation-transformation.html

#A (8, -2) -> A' (-2, 8)#

#vec(A'B) = sqrt((-2-5)^2 + (8+7)^2) = 16.55#

#color(purple)("Increase in distance " = 16.55 - 5.83 = 10.72#

Related questions
See all questions in Rotations
Impact of this question
1218 views around the world
You can reuse this answer
Creative Commons License