If a projectile is shot at an angle of #(5pi)/12# and at a velocity of #15 m/s#, when will it reach its maximum height??

1 Answer
Astralboy
Mar 22, 2017

10.711 meters

Explanation:

Split the velocity up into x-components and y-components:

#vx=15cos(5pi/12)#

#vy=15sin(5pi/12)#

We only care about the y-component in this case since we want to know maximum height. The initial velocity is #15sin(5pi/12)#. The final velocity will be #0# at the top. The acceleration is always #9.8# m/s downwards. We need to find d. Find a kinematics equation that has #vi#, #vf#, #a#, and #d#.

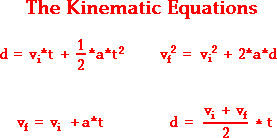
www.physicsclassroom.com

The equation in the top right corner has all four of those components. Plug into that equation:

#0=(15sin(5pi/12))^2+2(-9.8)(d)#

Solve for d:

#d=(-15sin(5pi/12))^2/((2)(-9.8))=10.711 m#

Related questions
See all questions in Falling Objects
Impact of this question
1817 views around the world
You can reuse this answer
Creative Commons License