How to solve this logarithmic function?
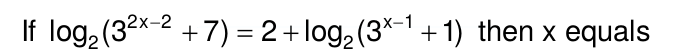
1 Answer
Explanation:
First, I would get both the logarithms on the same side.
#log_2(3^(2x-2)+7)-log_2(3^(x-1)+1)=2#
Now, use the rule
#log_2((3^(2x-2)+7)/(3^(x-1)+1))=2#
Rewrite by undoing the logarithm:
#(3^(2x-2)+7)/(3^(x-1)+1)=2^2=4#
Cross-multiply:
#3^(2x-2)+7=4(3^(x-1)+1)#
#3^(2x-2)+7=4(3^(x-1))+4#
#3^(2x-2)+3=4(3^(x-1))#
I stared at this for a little while before I realized something cool: that
#(3^(x-1))^2-4(3^(x-1))+3=0#
Now, we have a quadratic equation, if we let
#t^2-4t+3=0#
And solve as normal:
#(t-1)(t-3)=0#
#t=1,3#
Now we have to solve for
#3^(x-1)=1#
Take the logarithm:
#x-1=log_3(1)=0#
#x=1#
We also need the case
#3^(x-1)=3#
#x-1=log_3(3)=1#
#x=2#

