How do you use the binomial series to expand #(1 + 3x) ^8#?
1 Answer
Pascal's triangle.
Explanation:
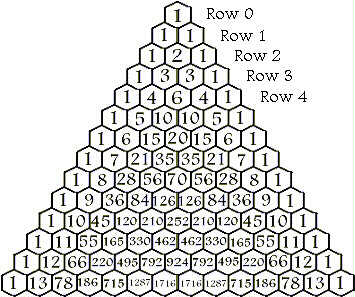
Since you're taking the binomial to the 8th power you would use the 8th row of this triangle and say that
and then add your exponents in a descending order so
and simplify.


