#(2sqrt5-4sqrt6)(3sqrt3+8sqrt2)#
Expand using the FOIL method.
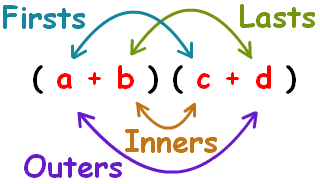
#(2sqrt5-4sqrt6)(3sqrt3+8sqrt2)=#
#color(blue)((2sqrt5*3sqrt3))+color(teal)((2sqrt5*8sqrt2))+color(red)((-4sqrt6*3sqrt3))+color(green)((-4sqrt6*8sqrt2)#
Multiply integers and square roots.
#color(blue)((2*3*sqrt5sqrt3))+color(teal)((2*8*sqrt5sqrt2))+color(red)((-4*3*sqrt6sqrt3))+color(green)((-4*8*sqrt6sqrt2))#
Simplify.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-12sqrt18))+color(green)((-32sqrt12))#
The first two sets of parentheses are cannot be simplified further. The second two sets of parentheses need further simplification.
Prime factorize #color(red)((-12sqrt18))#.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-12sqrt(2*3*3))+color(green)((-32sqrt12)#
Simplify.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-12*3sqrt2))+color(green)((-32sqrt12))#
Simplify.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-36sqrt2))+color(green)((-32sqrt12))#
Prime factorize #color(green)((-32sqrt12))#.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-36sqrt2))+color(green)((-32sqrt(2*2*3)))#
Simplify.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-36sqrt2))+color(green)((-32*2sqrt3))#
Simplify.
#color(blue)((6sqrt15))+color(teal)((16sqrt10))+color(red)((-36sqrt2))+color(green)((-64sqrt3))#
Simplify.
#6sqrt15+16sqrt10-36sqrt2-64sqrt3#

