How do you find the magnitude and direction of the electric field and magnetic field?

Ok, this is complicated...!

I would try using Lorentz Law:

#vecF=qvecE+qvecvxxvecB#

with the vector product:

I think in both cases you have a proton (with charge #q=1.6xx10^-19C#)!

1) at rest: #vecv=0#, the proton (its charge) is experiencing the #E# field around it and, as a consequence, the force:
#vecF=qvecE#
(#vecB=0#)
using moduli (say, along the #x# axis)
#E=F/q=(8.5xx10^-13)/(1.6xx10^-19)=5.3xx10^6V/m#
along the #x# direction and zero magnetic field.

2) Use the same approach with the given value of velocity remembering that now you'll have a magnetic field #vecB# perpendicular (due to the vector product) to the force (in the #x# direction) and velocity (in the #y# direction) and so in the #z# direction.

We need to consider the decrease in force so we need a negative value in the product: #qvecvxxvecB# (probably the #vecB# field will be in the negative #z# direction giving a negative modulus for the vector product).
We can write using our data into: #vecF=qvecE+qvecvxxvecB# considering the moduli:

#7.5xx10^-13=8.5xx10^-13+1.6xx10^-19*1.5xx10^6*B#
rearranging:
#B=-0.416~~-0.42T#

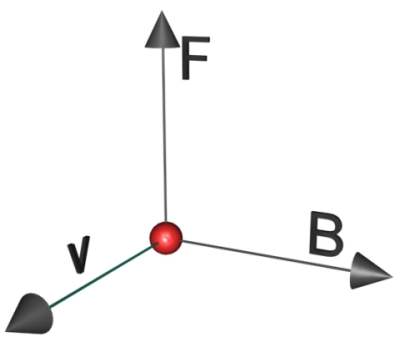
Here it is a possible visual representation: