How do you find the exact value of #cos( 2 arctan (5/12) )#?

1 Answer
mason m
Jun 8, 2016

#119/169#

Explanation:

Use the cosine double angle formula:

#cos(2x)=2cos^2(x)-1#

Here, inside the cosine function, the angle #arctan(5/12)# is being doubled, so we see that

#cos(2arctan(5/12))=2cos^2(arctan(5/12))-1#

To find #cos(arctan(5/12))#, draw a picture where #tan(beta)=5/12#, or where #5# is the opposite side's length and #12# is the adjacent side's length.

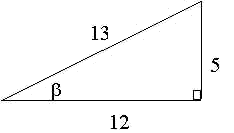
intmstat.com

In this triangle, #13# is the hypotenuse (through the Pythagorean Theorem), and #cos(beta)=12/13#. This also means that #cos(arctan(5/12))=12/13#.

So we see that

#2cos^2(arctan(5/12))-1=2(12/13)^2-1=288/169-1=119/169#

Related questions
See all questions in Basic Inverse Trigonometric Functions
Impact of this question
10621 views around the world
You can reuse this answer
Creative Commons License