How do you find #sin^-1 (cos(pi/6))#?

1 Answer
sankarankalyanam
Apr 18, 2018

#color(blue)(sin^-1 (cos (pi/6)) = pi/3 " or " 60^@#

Explanation:

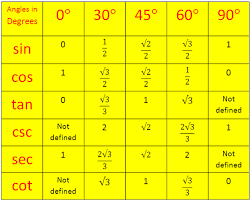
![www.math-only-math.com/images/http://trigonometrical-ratios-table.png](https://useruploads.socratic.org/Rod2GhDAR8qhxzUwIaKk_trigonometry%20values.png)

#"Let " theta = sin^-1 (cos (pi/6))#

From the table above, #cos (pi/6) = (sqrt3/2)#

#:. theta = sin^-1 (sqrt3/2)#

#sin theta = sqrt3/2#

But #sin 60 = sqrt3/2# as seen in the table.

Hence #color(blue)(theta = sin ^-1 (sin (60)) = 60^@ " or " pi/3#

Related questions
See all questions in Basic Inverse Trigonometric Functions
Impact of this question
15837 views around the world
You can reuse this answer
Creative Commons License