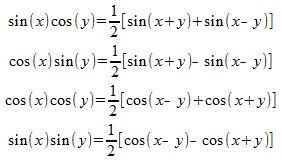How do you express #sin(pi/ 4 ) * sin( ( 2 pi) / 3 ) # without using products of trigonometric functions?

1 Answer
sankarankalyanam
Jul 3, 2018

#color(red)(=> [cos ((5pi)/12) - cos ((11pi)/12)]/2#

Explanation:

![https://study.com/academy/lesson/http://product-to-sum-identities-uses-applications.html](https://useruploads.socratic.org/2xBiCxzSmmCr1qNXSs2e_trigonometric%20identities.png)

#sin (pi/4) * sin ((2pi)/3)#

#sin x sin y = (1/2)[cos(x-y) - cos (x+y])#

#=> (1/2)[cos (pi/4 - (2pi)/3) - cos (pi/4 + (2pi)/3)]#

#=> [cos -((5pi)/12) - cos ((11pi)/12)]/2#

#color(red)(=> [cos ((5pi)/12) - cos ((11pi)/12)]/2#

Related questions
See all questions in Products, Sums, Linear Combinations, and Applications
Impact of this question
2169 views around the world
You can reuse this answer
Creative Commons License