How do i expand (1+x)(1+x)(1+x)(1+x) using binomial theorem?

We wish to expand

`(1+x)(1+x)(1+x)(1+x)=(1+x)^4`

Now, the Binomial Theorem states that it is possible to expand the sum of two numbers `x` and `y` raised to the power `n` into the form:

`(x+y)^n = sum_(k=0)^n ((n),(k))x^ky^(n-k)`

Where `((n),(k))` denotes the binomial coefficient, and is calculated by:

`((n),(k))=(n!)/(k!(n-k)!)`

If we substitute `y=1` into the formula, we have:

`(1+x)^n = sum_(k=0)^n ((n),(k)) x^k`

In our particular case, `n = 4`, hence:

`(1+x)^4 = sum_(k=0)^4 ((4),(k)) x^k=((4),(0))+((4),(1))x+...+((4),(4))x^4`

All that is left to do is calculate `((4),(k))` for `k=1,2,3` and `4`.

`{(((4),(0))=(4!)/(0!*4!)=24/(1*24)=1),(((4),(1))=(4!)/(1!*3!)=24/(1*6)=4),(((4),(2))=(4!)/(2!*2!)=24/(2*2)=6),(((4),(3))=(4!)/(3!*1!)=24/(6*1)=4),(((4),(4))=(4!)/(4!*0!) = 24/(24*1)=1) :}`

Finally,

`(1+x)^4 = 1+4x+6x^2+4x^3+x^4`

For small `n`, calculating every `((n),(k))` explicitly is ok, but for larger values, it's tedious, because the factorial function rapidly increases.

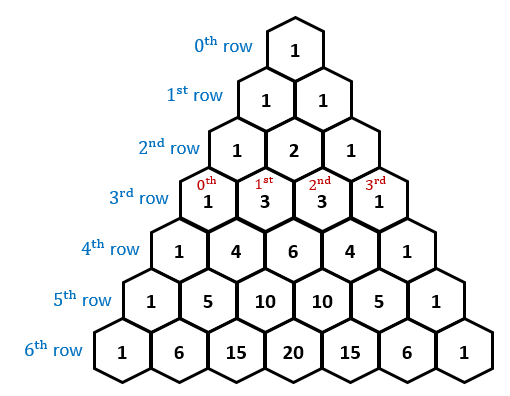
Instead, we might use Pascal's triangle to makes things simpler. Here it is:


This triangle is build up by adding; if we imagine near every `1` to be a `0` and if the element at the very top is `1`, then the next row will have elements `0+1=1` and `1+0=1`, because our top `1` has zeros to its right and left. Similarly, the second row values will be `0+1=1`, `1+1=2`, and `1+0=1`.

To see more on Pascal's triangle, check this link.

Another property of this triangle is that the `k`-th element on the `n`-th row is equal to `((n),(k))`. By this knowledge, we can easily judge that

`(1+x)^4 = 1+4x+6x^2+4x^3+x^4`

Here's a visual representation.