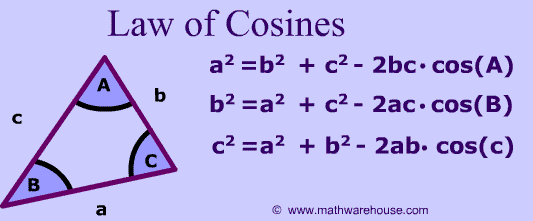Given a triangle with sides measuring 15in, 10in, and 12in; with angle C across from 10in, angle A across from 12in, and angle T across from 15in. How do you find the angle measures?
2 Answers
Explanation:
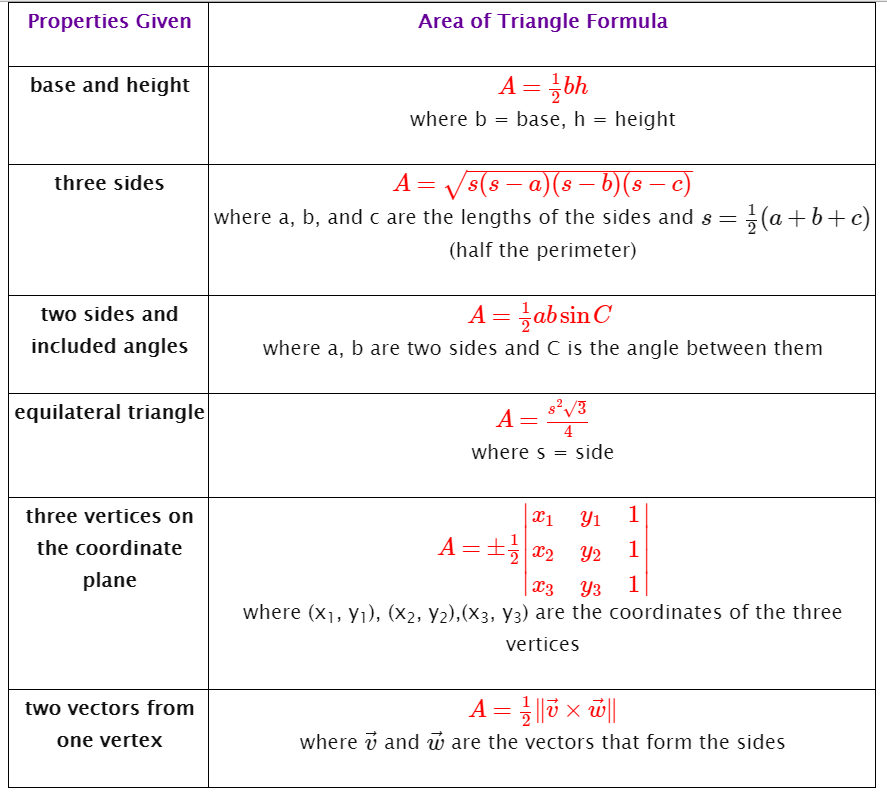
Explanation: