Let (r,theta)(r,θ) be the Polar coordinates of z_2z2. We have to find some sort of relations between the Polar coordinates and the Cartesian ones, which we know are (4,4)(4,4).
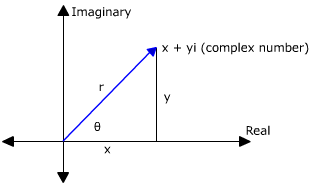
Let zeta=x+yiζ=x+yi be a complex number with polar coordinates (r,theta)(r,θ). We can represent it is:
 )
)
From the diagram above, we can deduce the following properties:
{(r^2=x^2+y^2),(x=rcostheta),(y=rsintheta):}
Let us return to our particular case, z_2 = 4+4i. Instead of brute-forcing it through the formulae, we can instead factor out the 4:
z_2 = 4(color(red)(1+i))
Now, in the complex plane, we know that 1 and i have the same magnitude, thus, the complex number 1+i forms a isosceles right triangle, with angle theta=pi"/"4.
Since both "Re"(z_2) and "Im"(z_2) are positive, our theta must be pi"/"4.
We know that for this type of triangle, the hypotenuse is the lenght of its side times sqrt2. The lenght of each of the legs in our triangle 4, as we have "Re"(z_2)="Im"(z_2)=4.
=> r=4sqrt2
Thus, the Polar coordinates of z_2 are (4sqrt2,pi/4).
In other words, z_2 = 4sqrt2e^(ipi/4), by Euler's identity.
 )
) 
