At which depth will the glass, which is it not a right cylinder, be volumetrically half-filled? Assume that the thickness of the base is negligible and the thickness of the walls is constant.
I think I would first have to find the derivative of perhaps the circular area or something like that... Out of the box answers are welcome:))
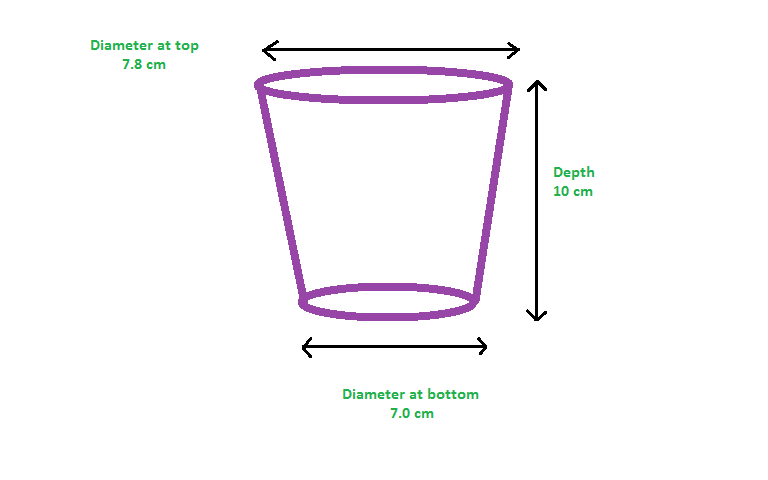
I think I would first have to find the derivative of perhaps the circular area or something like that... Out of the box answers are welcome:))

1 Answer
The split should occur at a height of approx
Explanation:
No Calculus required:
The mathematical name for the given "bucket" , or "glass" shape is a frustum, we can readily calculate the volume using the formula:
# V = pi/3(R^2 + rR + r^2)h \ \ \ # (See Notes)
We are required to split the volume of the given frustum of lower radius
Suppose the volumeatic split occurs at a height
Using this information, and utilising the frustum formula, we can write the identical volume of each frustum as:
# pi/3(3.5^2 + 3.5R + R^2)h = pi/3(R^2 + 3.9R + 3.9^2)(10-h) #
And by similar
# h : (R-3.5) = 10: (3.9-3.5) #
# :. h/(R-3.5) = 10/(0.4) #
# :. 0.4h = 10(R-3.5) #
# :. 0.4h = 10R-35 #
# :. 10R = 0.4h +35 #
Then we solve the two equations simultaneously, which results in the solution:
# h ~~ 5.26948# #R~~3.71078# (5dp)
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Notes:
We can readily derive the frustum volume by considering the difference in the volumes of standard cones#

