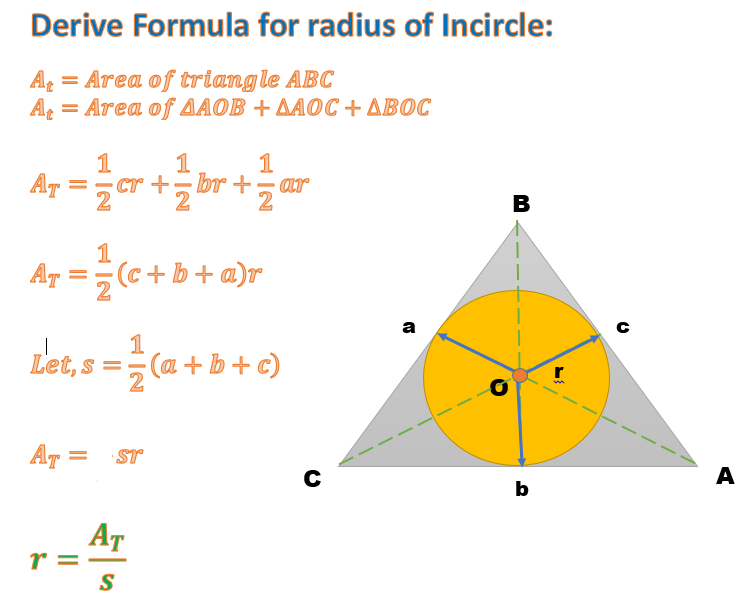
A triangle has corners at (5 , 2 ), (1 ,3 ), and (7 ,4 ). What is the radius of the triangle's inscribed circle?

1 Answer
sankarankalyanam
Jun 21, 2018

color(blue)("Radius of incircle " r = A_t / s = 5.0224 / 6.52 = 0.77 " units"

Explanation:

![http://mathibayon.blogspot.com/2015/01/http://derivation-of-formula-for-radius-of-incircle.html](https://useruploads.socratic.org/qByQYJn5SEeAPjtKhB4j_incircle%20radius.png)

"Incircle radius " r = A_t / s

A(5,2), B(1,3), C(7,4)

a = sqrt((7-1)^2 + (4-3)^2) = sqrt37

b = sqrt((7-5)^2 + (4-2)^2) = sqrt8

c = sqrt((5-1)^2 + ( 2-3)^2) = sqrt17

"Semi-perimeter " s = (a + b + c) / 2 = (sqrt37 + sqrt8 + sqrt17) / 2 = 6.52

"A_t = sqrt(s (s-a) s-b) (s-c))

A_t = sqrt(6.52 (6.52-sqrt37) (6.52 - sqrt8) (6.52 - sqrt17)) =5.0224

color(blue)("Radius of incircle " r = A_t / s = 5.0224 / 6.52 = 0.77 " units"

Related questions
See all questions in Area of Inscribed Triangle
Impact of this question
2542 views around the world
You can reuse this answer
Creative Commons License