A radioactive element has a half-life of 5 years. If you leave a 2 g sample of this element under your chemistry desk for 15 years, what mass will remain undecayed?

So, you know that your radioactive element has a nuclear half-life of #5# years.

As you know, a radioactive isotope's half-life tells you the time needed for half of an initial sample to undergo radioactive decay.

If you start with an initial sample #A_0#, you can say that you'll be left with

• #A_0 * 1/2 -># after one half-life
• #A_0/2 * 1/2 = A_0/4 -> # after two half-lives
• #A_0/4 * 1/2 = A_0/8 -># after three half-lives
  #vdots#

and so on. This means that you can express a relationship between the Initial sample of the radioactive isotope, #A_0#, and the amount that remains undecayed, #A#, in terms of how many half-lives pass in a given period of time

#color(blue)(A = A_0 * 1/2^n)" "#, where

#n# - the number of half-lives

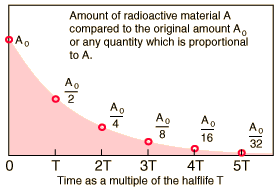
In your case, you can say that

#n = (15 color(red)(cancel(color(black)("years"))))/(5color(red)(cancel(color(black)("years")))) = 3#

This means that you'll be left with

#A = A_0 * 1/2^3 = 1/8 * A_0#

Therefore, your original sample will be down to #1/8"th"# of its initial value after the passing of #15# years

#A = 1/8 * "2 g" = color(green)("0.25 g")#

I'll leave the answer rounded to two sig figs.