 )
)
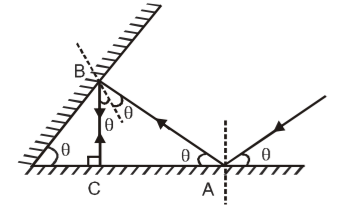
The two mirrors are inclined at an angle #theta#. The ray diagram has been drawn for an arbitrary angle. Actual angle need to be found out. As such actual ray diagram will be different.
It is clear that for third reflection the ray must hit the mirror normally or make angle of reflection #=0^@#
As dotted line at #B# is normal to the mirror, retracing the path from #C,# we see that four angles at point #B#, are
#90-theta#, (sum of three angles of a #Delta=180^@#)
#theta and theta#, (angles of incidence and of reflection)
#90-theta#, (straight line has angle #=180^@#)
Incident ray at #A# is parallel to the other mirror and dotted line is normal to mirror. This indicates angles #theta# at #A#
Now in triangle #ABC# sum of its three angles is equal to #180^@#. We have the equation
#90+(theta+theta)+theta=180#
#=>3theta=180-90#
#=>theta=30^@#
 )
)