Question #74b2b

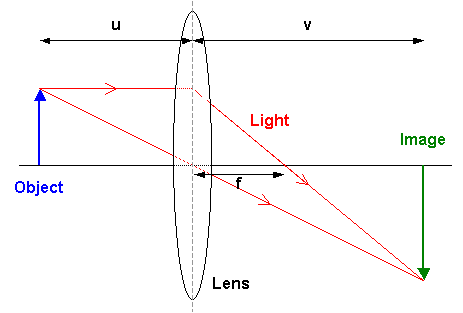
We know the conjugate foci relation of lens as follows

#color(blue)(1/v-1/u=1/f)#

Where

#u->"object distance"#

#v->"image distance"#

#f->"focal length"#

Imposing sign convention

#u=-u" for real object"#

#v=+v" for real image"#

#f=+f" for converging lens"#

So the lens formula becomes

#color(green)(1/v-1/(-u)=1/f)#

#=>color(green)(1/v+1/u=1/f)#

Now let us consider that the distance between real object and real image be #D#. This means #u+v=D#. So putting #v=D-u# in the lens equation we get

#color(red)(1/(D-u)+1/u=1/f)#

#color(red)(=>(u+D-u)/(u(D-u))=1/f)#

#color(red)(=>Df=(u(D-u)))#

#color(red)(=>u^2-Du+Df=0)#

This is a quadratic equation of #u#. For the formation of real images for real object the roots of this equation should be real.To satisfy this condition the discriminant of this equation must be #>=0#

So #color(violet)(D^2-4Df>=0)#

#color(violet)(=>D^2>=4Df)#

#color(violet)(=>D>=4f)#

From this relation we can conclude that the minimum distance between real obejct and its real image formed by a converging lens is #4f#

The following graph supports the phenomenon discussed above.