If one of the sides of a right angled triangle, whose all sides have integral values, is `12`, then what is the largest possible radius of its incircle?

Incircle in a right angled triangle is very special case. Infact it can be proved easily using the following figure (by joining incenter to the vertices of the triangle).


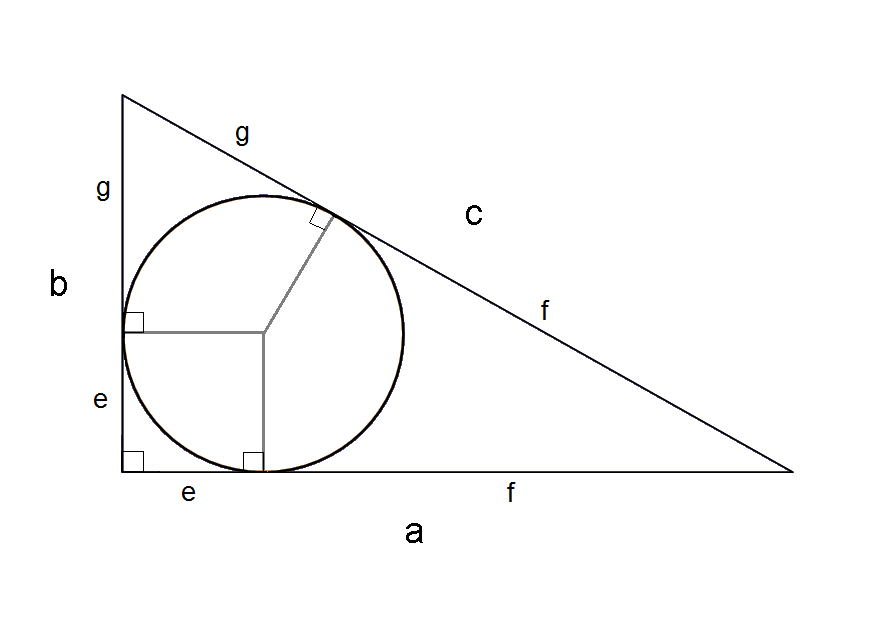
that radius of incircle is `(ab)/(a+b+c)` or `(a+b-c)/2`

As one of the side is `12`, let the other side be `x` and then hypotenuse is `sqrt(144+x^2` and radius of incircle is

`r(x)=(12+x-sqrt(144+x^2))/2` or `6+1/2(x-sqrt(144+x^2))`

Further if all sides are integers if `h` is hypotenuse and we have one side as `x`, then `144=h^2-x^2=(h+x)(h-x)` and sum of possible factors of `144` has to be even as `h` and `x` are integers.

Possible solutions are `2xx72`, `4xx36`, `6xx24`, `8xx18` and `12xx12`. The latter is not admissible as it results in one side to be `0`. The first four results give values of `(h,x)` as `(37,35)`, `(20,16)` `(15,9)` and `(13,5)`.

and for these we get `r={5,4,3,2}`

Hence, largest incircle possible is of radius `5` and dimensions of triagle are `(12,35,37)` and answer is D.