Question #6ffde

Osmotic pressure is simply the pressure that must be applied to a solution in order to prevent the incoming flow of water through a semipermeable membrane.


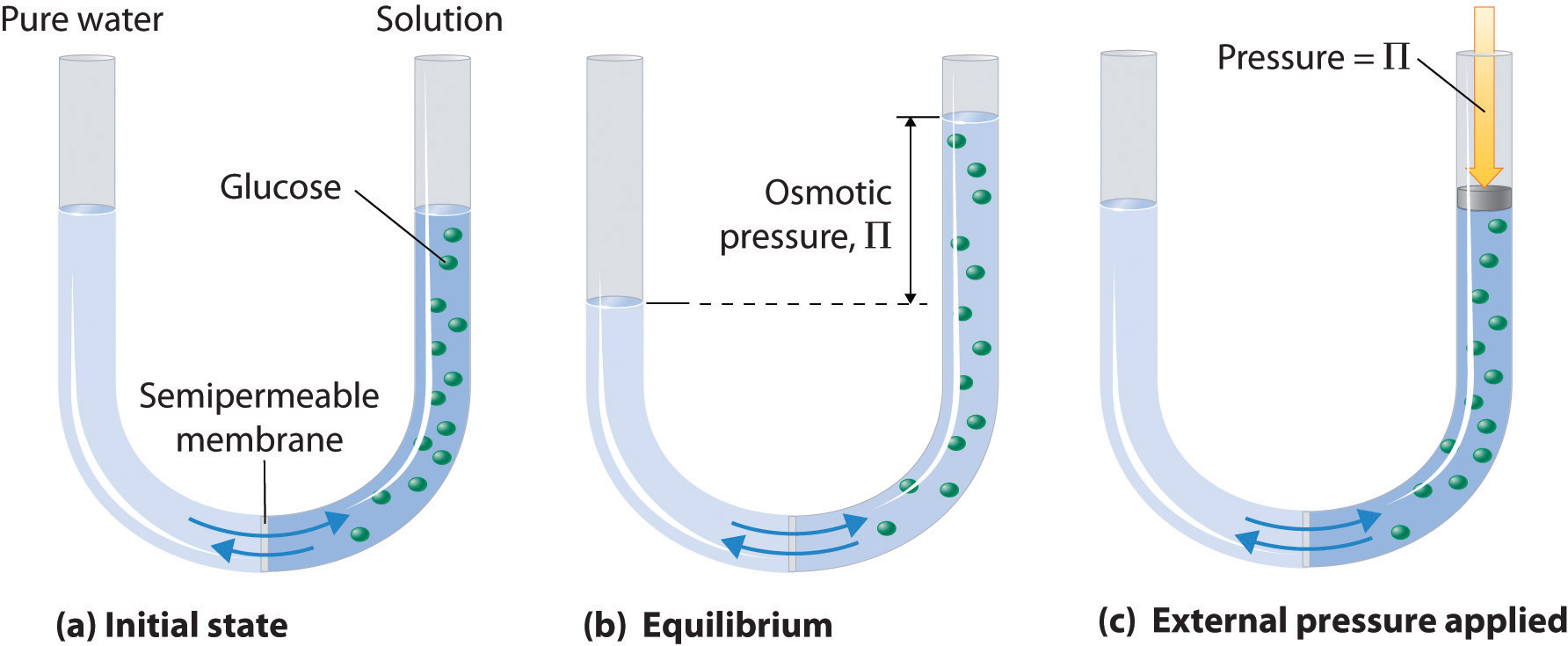
You can derive the equation that gives you the osmotic pressure of a solution that contains a non-electrolyte solute by using the ideal gas law equation

`color(blue)(|bar(ul(color(white)(a/a)PV = nRTcolor(white)(a/a)|)))" "`, where

`P` - the pressure of the gas
`V` - the volume it occupies
`n` - the number of moles of gas
`R` - the universal gas constant, usually given as `0.0821("atm" * "L")/("mol" * "K")`
`T` - the absolute temperature of the gas

Isolate `P` on one side of the equation to get

`P = n/V * RT`

Now, you know that the number of moles of solute per volume of solution gives you the molarity of the solution

`color(purple)(|bar(ul(color(white)(a/a)color(black)(c = n_"solute"/V_"solution")color(white)(a/a)|)))`

Plug this into the above equation to get the osmotic pressure, `Pi`

`color(blue)(|bar(ul(color(white)(a/a)Pi = c * RTcolor(white)(a/a)|)))`

Now, let's say that `M_Mcolor(white)(a)"g mol"^(-1)` is the molar mass of this protein. You can express the number of moles of solute in solution by writing

`n = (30.0 color(red)(cancel(color(black)("g"))))/(M_Mcolor(red)(cancel(color(black)("g")))"mol"^(-1)) = 30.0/M_Mcolor(white)(a)"moles"`

You thus have

`Pi = 30.0/M_M * 1/V * RT`

Isolate `M_M` on one side of the equation, convert the temperature from degrees Celsius to Kelvin, and plug in your values to get

`M_M = 30.0/Pi * (RT)/V`

`M_M = (30.0 color(red)(cancel(color(black)("moles"))))/(0.0167color(red)(cancel(color(black)("atm")))) * (0.0821(color(red)(cancel(color(black)("atm"))) * color(red)(cancel(color(black)("L"))))/(color(red)(cancel(color(black)("mol"))) * color(red)(cancel(color(black)("K")))) * (273.15 + 25)color(red)(cancel(color(black)("K"))))/(1.00 color(red)(cancel(color(black)("L"))))`

`M_M = "43,919"`

I'll leave the answer rounded to three sig figs and expressed in scientific notation

`M_M = color(green)(|bar(ul(color(white)(a/a)color(black)(4.39 * 10^4 "g mol"^(-1))color(white)(a/a)|)))`