Question #e121a

A radioactive isotope's nuclear half-life tells you how much time must pass before the half of the original sample undergoes decay.

In your case, the half-life of iodine-131 is 8 days. This means that any sample of iodine-131 that undergoes decay will be halved after 8 days, halved again after another 8 days, halved again after another 8 days, and so on.

You know that the fuel rods are stored underwater for 56 days. You can use this value to determine how many half-lives will pass.

#"no. of half-lives" = n_"half" = t/t_"1/2"#, where

#t_"1/2"# - the half-life of the element.

Plug in your values to get

#n_"half" = (56cancel("days"))/(8cancel("days")) = 7#

So, if the initial amount gets halved with every passing half-life, you can write

#A(t) = A_0/2^(n_"half")#

In your case, you have

#A(t) = A_0/2^7 = 1/128 * A_0#

This means that the fraction remaining after 56 days will be

#A(t)/A_0 = (1/128 * cancel(A[0]))/cancel(A[0]) = color(green)(1/128)#

The first thing to do is count how many half lives have elapsed.

The half life (#t_(1/2)# )is the time taken for half the amount of a given sample to decay.

You can see that 56 days is 7 half lives since 56/8 = 7

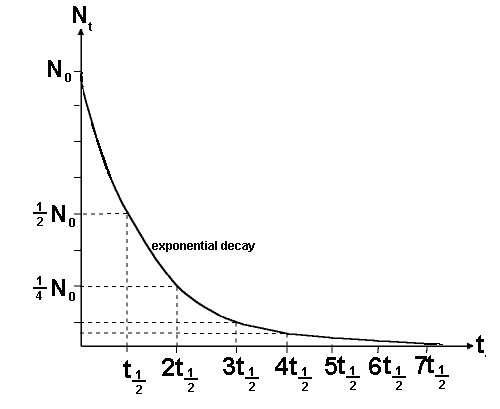
To get the fraction remaining we need to x by 1/2 seven times:

1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 = 1/128

If you don't get nice numbers like this you can use the equation for radioactive decay:

#N_t=N_0e^(-lambdat)#

#N_t# = no. atoms remaining

#N_0# = initial no. atoms

#t# = time elapsed

#lambda# = the decay constant.

We get the decay constant from the half life:

#lambda=(0.693)/(t_(1/2))#

#lambda = 0.693/8=0.0866d^(-1)#

Taking natural logs#rArr#

#ln((N_t)/(N_0))=-lambdaxxt=-0.0866xx56=-4.851#

From which #(N_t)/(N_0)=0.00782#

To compare this with the other method we can check the value of 1/128 = 0.00781 so that agrees quite nicely.