!! LONG ANSWER !!
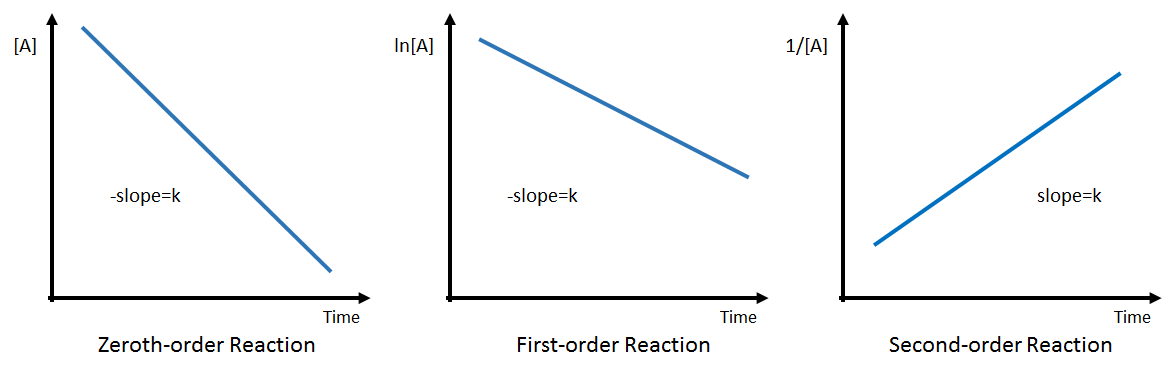
Let's start with point a). If you look at the graphs for zeroth, first, and second order reactions, you'll notice that only one of them has #"1/concentration"# plotted against time with a resulting positive slope.
 )
)
This means that, because the #1/([A]_0)# graph you plotted has a positive slope, your reaction can only be second-order. Since there is only one reactant, #"A"#, the rate law for your reaction can be written as
#"rate" = k * [A]^(2)#, where
#"k"# - the rate constant.
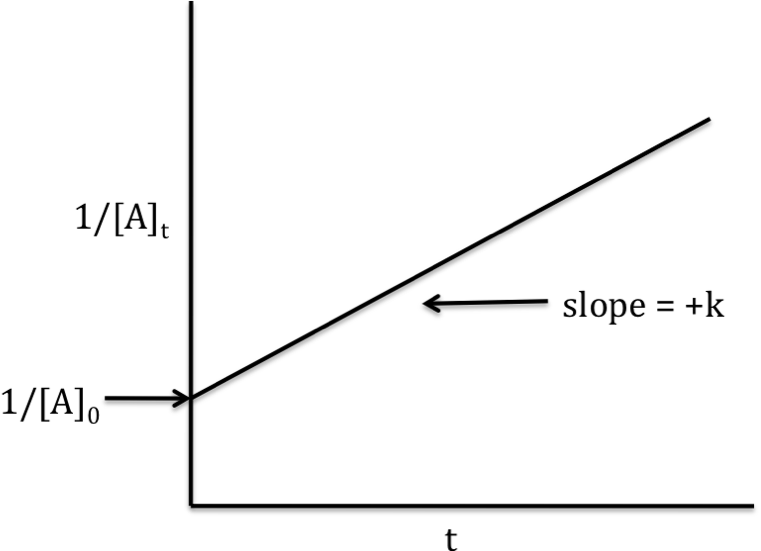
The trick here is to realize that the slope of the graph is equal to the rate constant k for this reaction.
 )
)
This means that your rate constant will be
#k = "slope" = 3.6 * 10^(-2)"L" * "mol"^(-1) * "s"^(-1)#
The integrated rate law for a second-order reaction looks like this
#1/([A]) - 1/([A]_0) = k* t#, where
#[A]# - the concetration of #"A"# after a time t has passed;
#[A]_0# - the initial concentration of #"A"#;
Moving on to point b). To determine the half-life of this reaction, replace #"t"# with #"t"_("1/2")# and #[A]# with #[A]_0/2# in the above equation. (Remember that, by definition, the reaction's half-life is the time needed for the reactant's initial concentration to be halved).
#1/([A]_0/2) - 1/([A]_0) = k * t_("1/2")#
Solving this for #t_("1/2")# will give you
#t_("1/2") = 1/(k * [A]_0)#
Plug in the values you have for k and #[A]_0# and you'll get
#t_("1/2") = 1/(3.6 * 10^(-2)"L" * "mol"^(-1) * "s"^(-1) * 2.8 * 10^(-3)"mol" * "L"^(-1))#
#t_("1/2") = 9.92 * 10^(3)"s"#
Finally, point c). Use the integrated rate law to solve for #"t"#, since you know that the value of #[A]# must now be #7.00 * 10^(-4)"M"#. So,
#1/(7.00 * 10^(-4)"M") - 1/(2.8 * 10^(-3)"M") = 3.6 * 18^(-2)"M"^(-1)"s"^(-1) * t#
#1071.43 "M"^(-1) = 3.6 * 18^(-2)"M"^(-1)"s"^(-1) * t#
#t = 1071.43/(3.6 * 10^(-2)"s"^(-1)) = "29761.94 s"#, or
#t = 2.976 * 10^(4)"s"#
Rounded to two sig figs, the answer will be
#t = 3.0 * 10^(4)"s"#
SIDE NOTE I didn't derive the integrated rate law for this second-order reaction because the answer would have been even longer, so I'll leave that to you as practice.
 )
)  )
) 
