How do you solve and find the value of #cos^-1(1/2)#?

2 Answers
Untitled
May 5, 2018

Refer to Explanation

Explanation:

#cos^-1(1/2) = 60^@#

Trigonometric Ratios of Special Angles:
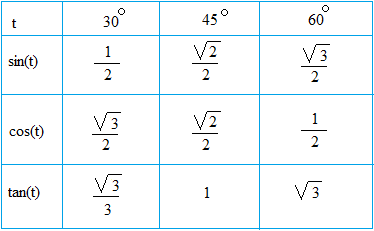
![https://www.basic-mathematics.com/http://trigonometric-ratios-of-special-angles.html](https://useruploads.socratic.org/CWElR8lRtm5IxQlgh4CQ_trigonometric-values-of-special-angles.png)

Nghi N
May 5, 2018

#pi/3; (5pi)/3#
#60^@; 300^@#

Explanation:

#cos x= 1/2#
Trig table gives -->
#x = pi/3#, or #x = 60^@#
Unit circle gives another arc (angle) that has the same cos value (1/2) -->
#x = - pi/3#, or #x = - 60^@#,
or #x = (5pi)/3# (co-terminal to #- pi/3#)

Related questions
See all questions in Inverse Trigonometric Properties
Impact of this question
14707 views around the world
You can reuse this answer
Creative Commons License