How do you find the exact value of sin 45 degrees?

Question

How do you find the exact value of sin 45 degrees?

2 Answers

Impact of this question

165852 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-28T10:38:36

$sin45^@=sqrt(2)/2$

Explanation:

This is a common value, in which $sin45^@=1/sqrt2$ .

We can now rationalize the fraction, which comes out to:

$1/sqrt2*1/1$

$=1/sqrt2*(sqrt(2))/sqrt2$

$=sqrt(2)/2$

Answer 2 · 2018-03-28T10:42:53

The exact value of $\sin(45)$ is $\frac{\sqrt{2}}{2}$ .

Explanation:

Consider $\triangle ABC$ to be right-angled in $B$ and choose $\angle BCA$ such that its measure is $45^o$ . Since the triangle is isosceles, we can deduce that angle $\angle CAB$ is also $45^o$ . Then pick an arbitrary value for $AB$ and $BC$ and apply the Pythagorean theorem. I'll go with the unit triangle, choosing both $AB$ and $BC$ to be $1$ (remember, the triangle is isosceles):

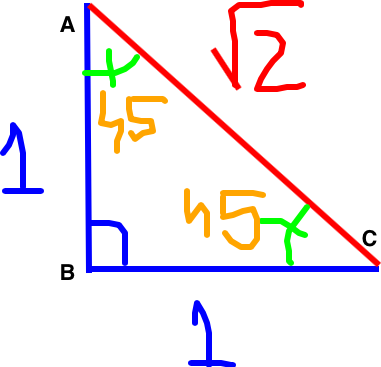
![A triangle and my great photoshop http://skills...](https://useruploads.socratic.org/T2tY81UJQZuErbiHQ6Gq_Unknown.png)

The hypothenuse $AC$ can easily be calculated now: $AC=\sqrt{BC^2+AB^2}=\sqrt{1^2+1^2}=\sqrt{2}$ .

The sine is defined as the ratio between the opposed side and the hypothenuse. Therefore, $\sin 45^o=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ .

In decimal form, it is roughly $0.7071067812$ .

Science

Math

Humanities

... and beyond

How do you find the exact value of sin 45 degrees?

2 Answers

Explanation:

Explanation:

Related questions

Impact of this question