Factorise (A^2- 1) (B^2- 1) + 4AB?

2 Answers
Watchmojo J.
Mar 1, 2018

(A-1)(A+1)(B-1)(B+1)+4AB

Explanation:

When multiplying out 2 brackets, you use this technique.

![https://www.youtube.com/watch?v=d0gKPnKy6YQ]
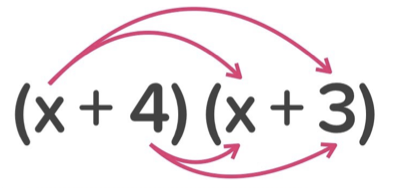(useruploads.socratic.org)

In this case, this is called the difference of 2 squares, which always produces this

(x-y)(x+y)

= x^2 - yx + yx -y^2

= x^2 -y^2

It will always give the square of one number minus the square of another.

It is the same for (A^2 - 1) and (B^2 - 1)

=((A)^2 - (1)^2)

((B)^2 - (1)^2)

Therefore, both can be factorised back into 2 brackets

(A-1)(A+1)

and

(B-1)(B+1)

So,

(A^2 - 1)(B^2 - 1) + 4AB

can be factorised to

(A-1)(A+1)(B-1)(B+1)+4AB

George C.
Mar 1, 2018

(A^2-1)(B^2-1)+4AB = (AB-A+B+1)(AB+A-B+1)

Explanation:

(A^2-1)(B^2-1)+4AB

= A^2B^2-A^2-B^2+1+4AB

= (A^2B^2+2AB+1)-(A^2-2AB+B^2)

= (AB+1)^2-(A-B)^2

= ((AB+1)-(A-B))((AB+1)+(A-B))

= (AB-A+B+1)(AB+A-B+1)

Related questions
Impact of this question
6149 views around the world
You can reuse this answer
Creative Commons License