#f(x) = 10 - x^2, x >= 0 #
To find the inverse, #f^(-1) (x)#, switch the variables #x# and #y# and solve for #y#.
#y = 10 - x^2#
#x = 10 - y^2# #-># switch variables
# x- 10 = - y^2#
# -x + 10 = y^2#
# y = +- sqrt(-x + 10)#
However, since the domain of #f(x)# is restricted to #x>=0# (only positive values of #x#), the range of #f^(-1)(x)# will be restricted to only positive values of #y#. Thus, we only take the positive square root above.
So, #f^(-1) (x) = sqrt(-x + 10)#.
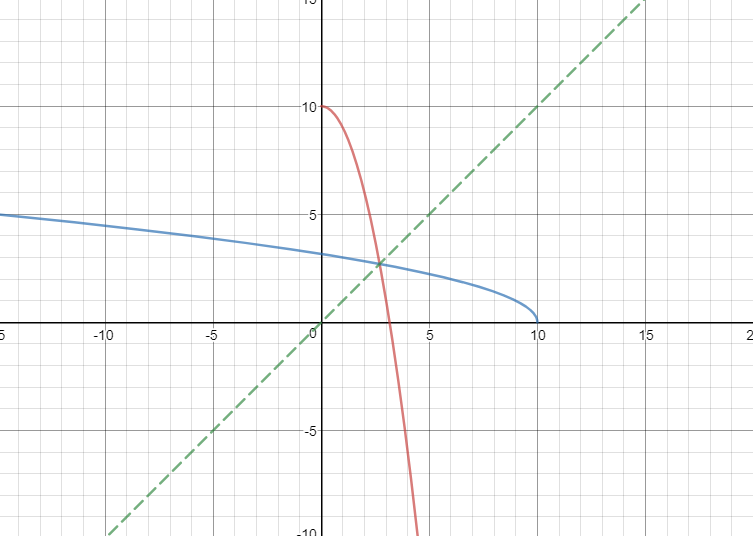
Any function and its inverse will be reflections of each other over the line #y = x#. Graphing #f(x)# and #f^(-1)(x)#, we can verify that they are indeed inverses.
 )
)
 )
) 
